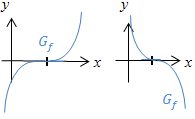Vielfachheiten der Nullstellen
Je nach dem, wie oft eine bestimmte Nullstelle bei einer Funktion 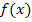 vorkommt, unterscheidet man einfache, doppelte, dreifache und vierfache usw. Nullstellen.
vorkommt, unterscheidet man einfache, doppelte, dreifache und vierfache usw. Nullstellen.
Ergibt die Gleichung 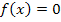 eine bestimmte Lösung genau ein einziges Mal, dann handelt es sich um eine einfache Nullstelle. Man sagt, die Nullstelle hat die Vielfachheit 1.
eine bestimmte Lösung genau ein einziges Mal, dann handelt es sich um eine einfache Nullstelle. Man sagt, die Nullstelle hat die Vielfachheit 1.
Ergibt sich aus 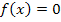 ein und dieselbe Lösung gleich zweimal, so ist es eine doppelte Nullstelle;die Vielfachheit dieser Nullstelle ist somit 2.
ein und dieselbe Lösung gleich zweimal, so ist es eine doppelte Nullstelle;die Vielfachheit dieser Nullstelle ist somit 2.
Entsprechend ist eine Nullstelle dreifach, wenn sie dreimal herauskommt, bzw. vierfach, wenn sie viermal herauskommt. Die Vielfachheit der Nullstelle ist dann 3 bzw. 4.
Besonders leicht lassen sich die Vielfachheiten der Nullstellen einer Polynomfunktion an ihrer faktorisierten Form (d.h. Produktform) ablesen. Siehe auch:Faktorisierter Funktionsterm
Man braucht nur den Exponenten außerhalb der einzelnen Klammern anschauen. Der Exponent entspricht der Vielfachheit der jeweiligen Nullstelle.
Beispiel: 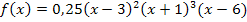
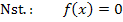
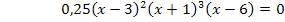
Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist. Daher braucht man nur die einzelnen Faktoren gleich Null zu setzen.
Der erste Faktor ist in unserem Beispiel 0,25. Er enthält kein x und kann somit gar nicht gleich Null werden;wir können ihn ignorieren.
Der zweite Faktor ist hier 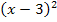 . Dieser Faktor wird gleich Null, wenn man für x die Zahl 3 einsetzt. Der Faktor kommt aber zum Quadrat vor;es handelt sich bei
. Dieser Faktor wird gleich Null, wenn man für x die Zahl 3 einsetzt. Der Faktor kommt aber zum Quadrat vor;es handelt sich bei 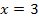 um eine doppelte Nullstelle. Man könnte schließlich statt
um eine doppelte Nullstelle. Man könnte schließlich statt 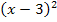 auch
auch 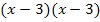 schreiben. Daran sieht man, dass die Lösung
schreiben. Daran sieht man, dass die Lösung 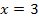 eigentlich zweimal herauskommt. Die erste Klammer
eigentlich zweimal herauskommt. Die erste Klammer 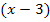 ergibt die erste Lösung
ergibt die erste Lösung 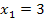 ;die zweite Klammer
;die zweite Klammer 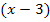 ergibt die zweite Lösung
ergibt die zweite Lösung 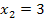 . Die Nullstelle
. Die Nullstelle 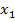 fällt praktisch mit der Nullstelle
fällt praktisch mit der Nullstelle 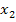 zusammen. Wir fassen dies als eine doppelte Nullstelle
zusammen. Wir fassen dies als eine doppelte Nullstelle 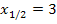 auf.
auf.
Der nächste Faktor ist 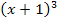 . Diese Klammer wird gleich Null, wenn man für x die Zahl -1 einsetzt. Die Klammer hat die Potenz 3. Daher handelt es sich um eine dreifache Nullstelle. Wir schreiben:
. Diese Klammer wird gleich Null, wenn man für x die Zahl -1 einsetzt. Die Klammer hat die Potenz 3. Daher handelt es sich um eine dreifache Nullstelle. Wir schreiben: 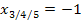
Der letzte Faktor ist 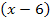 . Dieser Faktor wird gleich Null, wenn man für x die Zahl 6 einsetzt. Die Klammer ist ohne Potenz;Man kann sich aber den Exponent 1 dazu denken. Es handelt sich um eine einfache Nullstelle bei
. Dieser Faktor wird gleich Null, wenn man für x die Zahl 6 einsetzt. Die Klammer ist ohne Potenz;Man kann sich aber den Exponent 1 dazu denken. Es handelt sich um eine einfache Nullstelle bei 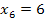 .
.
Die Funktion 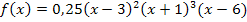 hat somit folgende Nullstellen:
hat somit folgende Nullstellen:
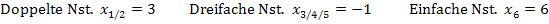
Zusammenhang zwischen Vielfachheit der Nullstelle und Verlauf des Graphen in der Umgebung der Nullstelle:
| Vielfachheit der Nullstelle: | Verlauf des Graphen 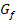 in der Umgebung der Nullstelle: in der Umgebung der Nullstelle: |
Skizze des Graphen 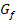 in der Umgebung der Nullstelle: in der Umgebung der Nullstelle: |
| Einfache Nullstelle
von |
Graph 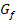 schneidet die x-Achse schneidet die x-Achse
mit Vorzeichenwechsel von |
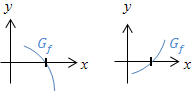 |
| Doppelte Nullstelle
von |
Graph 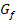 berührt die x-Achse berührt die x-Achse
ohne Vorzeichenwechsel von |
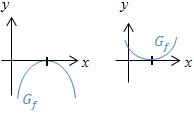 |
| Dreifache Nullstelle
von |
Graph 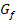 hat einen Terrassenpunkt hat einen Terrassenpunkt
(TEP) mit Vorzeichenwechsel von |
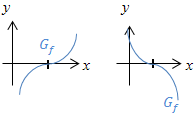 |
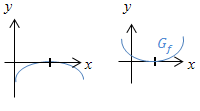
| Vierfache Nullstelle
von |
Graph 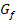 berührt die x-Achse;Graph berührt die x-Achse;Graph 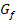 hat einen Flachpunkt (FLAP). Dies ist auch ein Extremum (HOP oder TIP) hat einen Flachpunkt (FLAP). Dies ist auch ein Extremum (HOP oder TIP)
Ähnlicher Verlauf wie bei einer doppelten Nullstelle, nur etwas „eckiger“. ohne Vorzeichenwechsel von |
 |
| Fünffache Nullstelle
von |
Graph 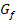 hat einen Terrassenpunkt. hat einen Terrassenpunkt.
Ähnlicher Verlauf wie bei einer dreifachen Nullstelle, nur etwas „eckiger“. mit Vorzeichenwechsel von |
|
| Sechsfache Nullstelle
von |
Graph 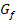 berührt die x-Achse;Graph berührt die x-Achse;Graph 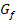 hat einen Flachpunkt (FLAP). Dies ist auch ein Extremum (HOP oder TIP) hat einen Flachpunkt (FLAP). Dies ist auch ein Extremum (HOP oder TIP)
Ähnlicher Verlauf wie bei einer doppelten oder vierfachen Nullstelle, nur noch etwas „eckiger“ als bei einer Vierfachen. ohne Vorzeichenwechsel von |
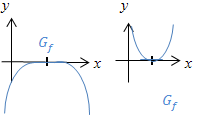 |
Es ist dir bestimmt schon aufgefallen:
Bei allen Nullstellen mit ungerader Vielfachheit wechselt 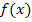 sein Vorzeichen. Bei den einfachen, dreifachen, fünffachen etc. Nullstellen liegt ein Vorzeichenwechsel von
sein Vorzeichen. Bei den einfachen, dreifachen, fünffachen etc. Nullstellen liegt ein Vorzeichenwechsel von 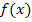 vor. Der Graph
vor. Der Graph 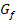 kommt von oben an die x-Achse heran und geht nach der Nullstelle unten weiter oder genau umgekehrt, er kommt von unten und geht dann oben weiter.
kommt von oben an die x-Achse heran und geht nach der Nullstelle unten weiter oder genau umgekehrt, er kommt von unten und geht dann oben weiter.
Bei allen Nullstellen mit gerader Vielfachheit liegt dagegen kein Vorzeichenwechsel von 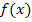 vor;so zum Beispiel bei den doppelten, vierfachen und sechsfachen Nullstellen. Der Graph
vor;so zum Beispiel bei den doppelten, vierfachen und sechsfachen Nullstellen. Der Graph 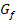 kommt von unten an die x-Achse heran und geht nach der Nullstelle wieder unten weiter bzw. er kommt von oben und geht nach der Nullstelle wieder oben weiter.
kommt von unten an die x-Achse heran und geht nach der Nullstelle wieder unten weiter bzw. er kommt von oben und geht nach der Nullstelle wieder oben weiter.
Nullstelle mit ungerader Vielfachheit  Vorzeichenwechsel von
Vorzeichenwechsel von 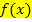
Nullstelle mit gerader Vielfachheit  kein Vorzeichenwechsel von
kein Vorzeichenwechsel von 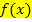
Nur für Schüler, welche die erste und auch höhere Ableitungen im Unterricht bereits behandelt haben:
Liegt an der Stelle 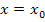 eine Nullstelle vor, gilt natürlich
eine Nullstelle vor, gilt natürlich 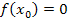 . Das ist nur eine andere Schreibweise für y = 0. Eine Nullstelle liegt schließlich auf der x-Achse und jeder Punkt der x-Achse hat die y-Koordinate 0. (Mit
. Das ist nur eine andere Schreibweise für y = 0. Eine Nullstelle liegt schließlich auf der x-Achse und jeder Punkt der x-Achse hat die y-Koordinate 0. (Mit 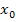 ist übrigens eine konkrete Zahl gemeint, hier eben die x-Koordinate der jeweiligen Nullstelle.)
ist übrigens eine konkrete Zahl gemeint, hier eben die x-Koordinate der jeweiligen Nullstelle.)
Ob auch die erste Ableitung 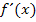 an der Stelle
an der Stelle 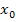 gleich Null ist, hängt davon ab, welche Vielfachheit die Nullstelle besitzt. Nur wenn die Tangente an
gleich Null ist, hängt davon ab, welche Vielfachheit die Nullstelle besitzt. Nur wenn die Tangente an 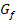 an der Stelle
an der Stelle 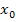 waagrecht verläuft, ist die Steigung und somit die erste Ableitung an dieser Stelle gleich Null. Ab einer Vielfachheit von 2 ist dies der Fall.
waagrecht verläuft, ist die Steigung und somit die erste Ableitung an dieser Stelle gleich Null. Ab einer Vielfachheit von 2 ist dies der Fall.
Die zweite Ableitung 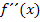 entspricht bekanntlich der Krümmung des Graphen
entspricht bekanntlich der Krümmung des Graphen 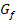 . Ab einer Vielfachheit von 3 ist die zweite Ableitung an der Stelle
. Ab einer Vielfachheit von 3 ist die zweite Ableitung an der Stelle 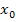 ebenfalls gleich Null.
ebenfalls gleich Null.
Die dritte Ableitung 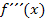 ist an der Stelle
ist an der Stelle 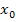 gleich Null ab einer Vielfachheit von 4.
gleich Null ab einer Vielfachheit von 4.
Zusammenfassung:
Bei einer einfachen Nullstelle gilt: 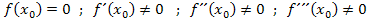
Bei einer doppelten Nullstelle gilt: 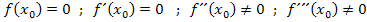
Bei einer dreifachen Nullstelle gilt: 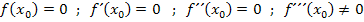
Bei einer vierfachen Nullstelle gilt: 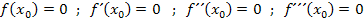
Wie man die Nullstellen einer ganzrationalen Funktion berechnet, auch wenn sie noch nicht in ihrer faktorisierten Form / Produktform gegeben ist, wird an Hand vieler Beispiele erklärt im Kapitel Polynomfunktionen / Ganzrationale Funktionen dritten und höheren Grades.
Die Berechnung der Nullstellen und ihrer Vielfachheiten ist ein Teil der Kurvendiskussion.