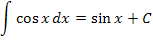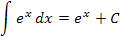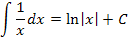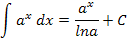Unbestimmtes Integral
Das unbestimmte Integral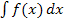 
entspricht der Menge aller Stammfunktionen 
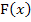einer Funktion 
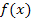. Es gilt: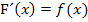 
Eine Funktion F(x) ist genau dann Stammfunktion zu 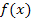, wenn ihre Ableitung F´(x) genau die Funktion 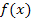ergibt. Das unbestimmte Integral ist nur eine andere Schreibweise für 
.
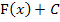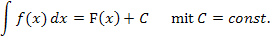
Wichtig:Bei einem unbestimmten Integral musst du unbedingt „+ C „ dazu schreiben, wenn du integriert hast!
Beispiel: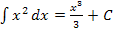 
Unbestimmte Integrale der Form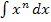 
werden berechnet, indem man zum Exponenten 1 dazu zählt und außerdem durch den neuen Exponenten teilt:
 |
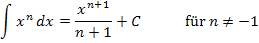Weitere wichtige Grundintegrale:
|
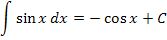
Eine multiplikative Konstante a darf vor das Integral gezogen werden. Es gilt nämlich:
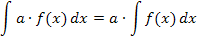
Beispiel: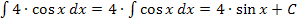 
Eine multiplikative Konstante ist eine konkrete Zahl ohne x, welche mit irgendetwas multipliziert wird. Solche Zahlen werden daher beim Integrieren einfach abgeschrieben;nur die restliche Funktion wird integriert.
Summen und Differenzen zweier Funktionen 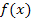und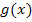 
dürfen einzeln, also Funktion für Funktion, integriert werden:
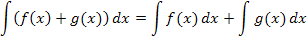
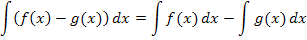
Beispiel: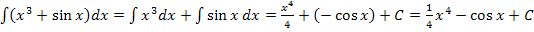 
Aber Vorsicht:Produkte und Quotienten zweier Funktionen dürfen dagegen keinesfalls einzeln integriert werden.
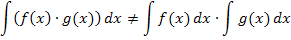
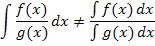
Wenn möglich bei einem Produkt immer zuerst ausmultiplizieren und danach integrieren. Beim Integral eines Quotienten den Bruch falls möglich ausrechnen, indem man jeden Summanden des Zählers einzeln durch den kompletten Nenner teilt. (Dabei kann eine Polynomdivisionnötig sein.) Dann erst integrieren.
Beispiele: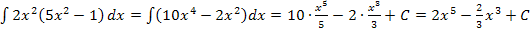 
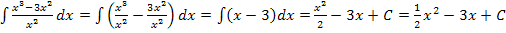
Lässt sich ein Produkt nicht ausmultiplizieren oder es liegt ein Bruch vor, der sich nicht ausrechnen lässt, muss man sich etwas anderes einfallen lassen. Leider gibt es keine richtige „Produktregel“ und „Quotientenregel“ zum Integrieren. Es gibt nur die sogenannte partielle Integration und die Integration durch Substitution. Diese beiden Integrationsregeln stehen in Bayern aber nicht auf dem Lehrplan des G8, nur Schüler einer mathematisch-technischen FOS oder BOS lernen das. (Erklärungen zur Integration durch Substitution und zur partiellen Integration gibt es im Kapitel Einführung in die Integralrechnung am Ende des Teils Weitere Integrationsregeln.)
Wenn du in eine bayerisches Gymnasiums G8 gehst, musst du dafür in der 12. Klasse die Integration von lineartransformierten Funktionen lernen. Das sind Integrale von Grundfunktionen, bei denen an Stelle von x eine lineare Funktion (Gerade), also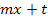 
vorkommt. Für solche Funktionen gilt:
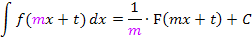
Beispiele: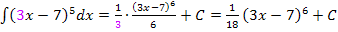 
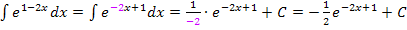
Weitere Erklärungen und Beispiele zur Integration linear transformierter Funktionen gibt´s bei Weitere Integrationsregeln.
Für die Integration von Quotienten steht eine wichtige Formel auf dem Lehrplan für Gymnasium G8 und mathematisch-technischer Zweig der FOS/BOS:
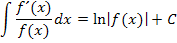
Der Zähler des Bruchs muss also die Ableitung des Nenners (oder ein Vielfaches davon) sein, damit die Formel angewendet werden kann.
Beispiele: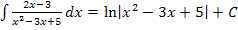 
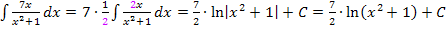
Anspruchsvollere Beispiele zur Integration mit Hilfe der Formel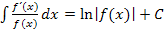 
kannst du dir anschauen bei Weitere Integrationsregeln.
