Unbestimmte Ausdrücke

Wenn man einen Grenzwert berechnen muss, kann es passieren, dass man auf einen sogenannten „unbestimmten Ausdruck“ stößt. Das ist ein Ausdruck, bei dem sich nicht allgemein sagen lässt, was herauskommt.

Zu den unbestimmten Ausdrücken zählen Ausdrücke der Form:

(Von den Vorzeichen wurde hier abgesehen. Statt 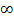kann auch 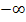vorkommen.)

Bei unbestimmten Ausdrücken kann man nicht generell sagen, was heraus kommt! Das Ergebnis so eines Ausdrucks kann Null, Unendlich bzw. Minus-Unendlich oder eine konkrete Zahl sein.

Das Ergebnis kann nur im jeweiligen Einzelfall ermittelt werden. Es hängt bei 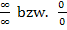davon ab, welches 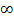bzw. welche 0 sich durchsetzt, also von welcher Funktion das jeweilige 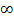bzw. die Null kommt. Bei 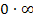ist zu überlegen, ob sich die Null gegenüber dem Unendlich durchsetzt oder entsprechend umgekehrt. Aber wie geht das?

Grundsätzlich gilt:

Die e-Funktion (siehe auch:Exponentialfunktion) wächst schneller als jedes Polynom oder eine ln-Funktion.

Die ln-Funktion wächst dagegen langsamer als jedes Polynom und die e-Funktion.

Merke:Die e-Funktion überwiegt, die ln-Funktion unterliegt!

In anderen Worten:

Ein Unendlich, das von einer e-Funktion kommt, ist stärker als ein Unendlich von einer Polynomfunktion oder einer ln-Funktion. Ebenso überwiegt eine Null, die von einer e-Funktion kommt, immer im Vergleich zu einer Null, die von einer Polynomfunktion kommt. Umgekehrt unterliegt das Unendlich, welches von einer ln-Funktion kommt, im Vergleich zu einem Unendlich, das von einer Polynomfunktion oder einer e-Funktion kommt.

Bei ist beispielsweise zu beurteilen, ob der Zähler oder der Nenner schneller gegen Unendlich strebt, also ob der Zähler oder der Nenner schneller wächst:

Geht der Zähler schneller gegen Unendlich als der Nenner, so gilt: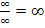

Wächst der Nenner schneller als der Zähler, so gilt: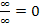

Sind Zähler und Nenner jeweils gleich stark, weil sie zum Beispiel beide eine e-Funktion enthalten oder beide ein Polynom gleichen Grades, dann hilft es in der Regel, wenn man jeweils die höchste Potenz mit x im Zähler und Nenner ausklammert und danach wegkürzt. Danach lässt sich der Grenzwert eindeutig berechnen. Es ergibt sich dann nämlich kein unbestimmter Ausdruck mehr. Das Ergebnis des Grenzwertes ist in diesem Fall eine konkrete reelle Zahl.

Bei 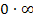ist zu überlegen, ob sich die Null gegenüber dem Unendlich durchsetzt oder entsprechend umgekehrt.

Kommt die Null von einer e-Funktion und das Unendlich von einer Polynomfunktion oder einer ln-Funktion, so überwiegt die Null und es gilt: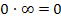

Kommt dagegen das Unendlich von einer e-Funktion und die Null zum Beispiel von einer gebrochenrationalen Funktion, so überwiegt das Unendlich und es gilt: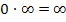

Manchen Lehrern reicht es, wenn man sich den Grenzwert, der zu einem unbestimmten Ausdruck führt, nach der oben beschriebenen Art überlegt.

---