Umkehrfunktion
Mit  wird die sogenannte Umkehrfunktion einer Funktion f bezeichnet. Dabei ist -1 allerdings nicht als Exponent zu sehen;es handelt sich nur um eine mathematische Schreibweise, die zugegebenermaßen leicht missverstanden werden kann. Im Gegensatz zu
wird die sogenannte Umkehrfunktion einer Funktion f bezeichnet. Dabei ist -1 allerdings nicht als Exponent zu sehen;es handelt sich nur um eine mathematische Schreibweise, die zugegebenermaßen leicht missverstanden werden kann. Im Gegensatz zu 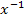 , was tatsächlich eine Potenz von x darstellt, ist
, was tatsächlich eine Potenz von x darstellt, ist  nur eine Schreibweise bzw. Bezeichnung für die Umkehrfunktion. (Man hätte auch eine andere Schreibweise, wie zum Beispiel
nur eine Schreibweise bzw. Bezeichnung für die Umkehrfunktion. (Man hätte auch eine andere Schreibweise, wie zum Beispiel 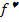 oder
oder 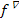 wählen können, doch irgendjemand hat sich wohl für
wählen können, doch irgendjemand hat sich wohl für  entschieden.) Obwohl
entschieden.) Obwohl 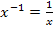 ist, ist
ist, ist  nicht das Selbe wie
nicht das Selbe wie 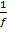 .
.
Was ist aber nun die Umkehrfunktion?
Die Umkehrfunktion  zu einer gegebenen Funktion f ist die Funktion, die sich mit der Funktion f wieder aufhebt. So ist beispielsweise die Wurzelfunktion
zu einer gegebenen Funktion f ist die Funktion, die sich mit der Funktion f wieder aufhebt. So ist beispielsweise die Wurzelfunktion 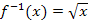 die Umkehrfunktion der Quadratfunktion f(x) =
die Umkehrfunktion der Quadratfunktion f(x) = 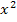 (mit
(mit 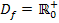 ). Umgekehrt ist auch die Quadratfunktion die Umkehrfunktion der Wurzelfunktion. Sie sind also gegenseitig Funktion und Umkehrfunktion.
). Umgekehrt ist auch die Quadratfunktion die Umkehrfunktion der Wurzelfunktion. Sie sind also gegenseitig Funktion und Umkehrfunktion.
Ein anderes, für Schüler der gymnasialen Oberstufe wichtiges Beispiel sind die Funktionen f(x) = 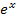 und
und  (x) = lnx. Auch sie sind Umkehrfunktionen zueinander, da sie sich gegenseitig aufheben:
(x) = lnx. Auch sie sind Umkehrfunktionen zueinander, da sie sich gegenseitig aufheben:![]()
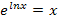
![]()
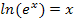
Mehr zu den Funktionen f(x) = 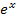 und
und  (x) = lnx findest du im Bereich Analysis in den Kapiteln Die Exponentialfunktion f(x) =
(x) = lnx findest du im Bereich Analysis in den Kapiteln Die Exponentialfunktion f(x) = 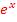 und Der natürliche Logarithmus f(x) = lnx
und Der natürliche Logarithmus f(x) = lnx
Ermittlung der Umkehrfunktion:
Graphisch ermittelt man die Umkehrfunktion durch Spiegelung des Graphen 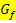 der Funktion f(x) an der Winkelhalbierenden des I. und III. Quadranten, d.h. durch Spiegelung an der Gerade y = x. Das Spiegeln von
der Funktion f(x) an der Winkelhalbierenden des I. und III. Quadranten, d.h. durch Spiegelung an der Gerade y = x. Das Spiegeln von 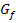 an der Winkelhalbierenden lässt sich am besten bewerkstelligen, indem man einen Punkt von
an der Winkelhalbierenden lässt sich am besten bewerkstelligen, indem man einen Punkt von 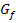 mit gut ablesbaren Koordinaten sucht, die x- und y-Koordinaten miteinander vertauscht und diesen Punkt dann in das Koordinatensystem einzeichnet. So verfährt man mit weiteren Punkten von
mit gut ablesbaren Koordinaten sucht, die x- und y-Koordinaten miteinander vertauscht und diesen Punkt dann in das Koordinatensystem einzeichnet. So verfährt man mit weiteren Punkten von 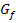 . Die Punkte mit den vertauschten x- und y-Koordinaten liegen alle auf dem Graphen der Umkehrfunktion, der nun leicht eingezeichnet werden kann. Das Vertauschen von x- und y-Koordinaten entspricht also der Spiegelung an der Winkelhalbierenden. Dabei werden aus senkrechten Asymptoten logischerweise senkrechte Asymptoten und umgekehrt.
. Die Punkte mit den vertauschten x- und y-Koordinaten liegen alle auf dem Graphen der Umkehrfunktion, der nun leicht eingezeichnet werden kann. Das Vertauschen von x- und y-Koordinaten entspricht also der Spiegelung an der Winkelhalbierenden. Dabei werden aus senkrechten Asymptoten logischerweise senkrechte Asymptoten und umgekehrt.
Beispiel:
Gegeben ist die Funktion f(x) = -2x + 2. Es soll der Graph der Umkehrfunktion graphisch ermittelt werden.
Lösung:
Auf dem Graph 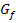 (Gerade mit der Steigung m = -2 und dem y-Achsenabschnitt t = 2 in der Abbildung unten blau dargestellt) liegt der Punkt P(0|2). Wir vertauschen die x- und y-Koordinate miteinander und erhalten den Punkt
(Gerade mit der Steigung m = -2 und dem y-Achsenabschnitt t = 2 in der Abbildung unten blau dargestellt) liegt der Punkt P(0|2). Wir vertauschen die x- und y-Koordinate miteinander und erhalten den Punkt 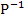 (2|0), welcher auf dem Graph der Umkehrfunktion
(2|0), welcher auf dem Graph der Umkehrfunktion 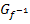 (in der Abbildung rot dargestellt) liegt. Ebenso verfahren wir beispielsweise mit dem Punkt Q(1|0) des Graphen
(in der Abbildung rot dargestellt) liegt. Ebenso verfahren wir beispielsweise mit dem Punkt Q(1|0) des Graphen 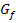 . Vertauschen der Koordinaten ergibt den Punkt
. Vertauschen der Koordinaten ergibt den Punkt 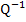 (0|1) des Graphen der Umkehrfunktion
(0|1) des Graphen der Umkehrfunktion 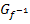 . Durch die beiden Punkte
. Durch die beiden Punkte 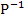 und
und 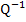 muss der Graph der Umkehrfunktion verlaufen. Außerdem muss der Schnittpunkt des Graphen
muss der Graph der Umkehrfunktion verlaufen. Außerdem muss der Schnittpunkt des Graphen 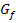 mit der Winkelhalbierenden y = x ebenfalls auf der Umkehrfunktion liegen, da alle Punkte der Winkelhalbierenden durch Spiegelung an ihr wieder auf sich selbst abgebildet werden. Daher schneiden sich Funktion und Umkehrfunktion immer genau auf der Winkelhalbierenden.
mit der Winkelhalbierenden y = x ebenfalls auf der Umkehrfunktion liegen, da alle Punkte der Winkelhalbierenden durch Spiegelung an ihr wieder auf sich selbst abgebildet werden. Daher schneiden sich Funktion und Umkehrfunktion immer genau auf der Winkelhalbierenden.
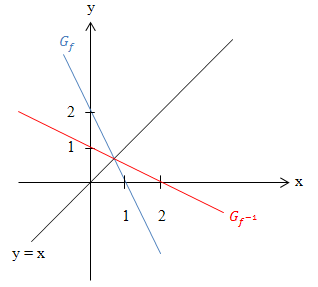
Rechnerisch lässt sich die Funktionsgleichung der Umkehrfunktion 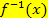 ermitteln, indem man x und y vertauscht und dann wieder nach y auflöst. (Manche Lehrer lösen die Funktionsgleichnung f(x) zuerst nach x auf und vertauschen dann erst x und y gegeneinander;das führt natürlich zum gleichen Ergebnis.) Durch das Vertauschen von x und y, vertauschen sich allerdings auch Definitions- und Wertemenge:
ermitteln, indem man x und y vertauscht und dann wieder nach y auflöst. (Manche Lehrer lösen die Funktionsgleichnung f(x) zuerst nach x auf und vertauschen dann erst x und y gegeneinander;das führt natürlich zum gleichen Ergebnis.) Durch das Vertauschen von x und y, vertauschen sich allerdings auch Definitions- und Wertemenge: 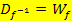
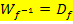
Beispiel:
Gegeben ist die Funktion f(x) = -2x + 2. Es soll die Gleichung der Umkehrfunktion 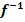 (x) rechnerisch ermittelt werden.
(x) rechnerisch ermittelt werden.
Lösung:
Statt f(x) schreiben wir zuerst y. Danach werden x und y gegeneinander vertauscht. Zuletzt wird wieder nach y aufgelöst.
y = -2x + 2
x = -2y + 2 |-2
x – 2 = -2y | 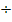 (-2)
(-2)
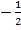 x +1 = y
x +1 = y
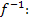 y =
y = 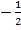 x +1 bzw.
x +1 bzw. 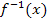 =
= 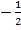 x +1
x +1
Nicht alle Funktionen sind umkehrbar. Nur Funktionen, deren Umkehrung auch wieder eine Funktion ergeben, nennt man umkehrbar.
In anderen Worten:Eine Funktion, die gespiegelt an der Winkelhalbierenden y = x, wieder eine Funktion ergibt, heißt umkehrbar. (Zur Erinnerung:Eine Funktion ordnet jedem x genau ein y zu! Beim Graph der Umkehrfunktion dürfen also keinesfalls zwei Punkte senkrecht übereinander liegen.)
Die Funktion f(x) = 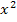 (Normalparabel mit Scheitel im Ursprung) ist beispielsweise in ihrer gesamten Definitionsmenge
(Normalparabel mit Scheitel im Ursprung) ist beispielsweise in ihrer gesamten Definitionsmenge  nicht umkehrbar, da ihre Umkehrung keine Funktion mehr darstellt. Vergleiche dazu die folgende Abbildung!
nicht umkehrbar, da ihre Umkehrung keine Funktion mehr darstellt. Vergleiche dazu die folgende Abbildung!
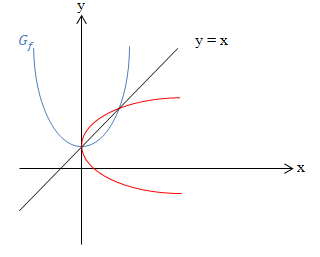
![]()
Anmerkung:Jeder einzelne Ast der Parabel für sich genommen ist allerdings schon umkehrbar. Schränkt man die Definitionsmenge der Funktion f(x) = 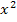 so ein, dass gilt
so ein, dass gilt 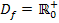 oder
oder 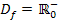 , lässt sich die Funktion umkehren. Die Umkehrfunktion zu f(x) =
, lässt sich die Funktion umkehren. Die Umkehrfunktion zu f(x) = 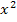 mit
mit 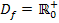 ist die Wurzelfunktion
ist die Wurzelfunktion 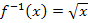 . Die Umkehrfunktion zu f(x) =
. Die Umkehrfunktion zu f(x) = 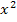 mit
mit 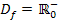 ist dagegen die negative Wurzelfunktion
ist dagegen die negative Wurzelfunktion 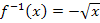 .
.
Nachweis der Umkehrbarkeit einer Funktion:
Eine Funktion ist genau dann umkehrbar, wenn jedem y-Wert der Funktion f(x) genau ein x-Wert zugeordnet wird. Auch wenn eine Funktion streng monoton ist, also entweder nur streng monoton steigend oder nur streng monoton fallend ist, dann ist sie sicher umkehrbar. Wenn bewiesen werden soll, dass eine gegebene Funktion f(x) umkehrbar ist, muss nur gezeigt werden, dass sie streng monoton ist. Das geschieht am einfachsten mit Hilfe der ersten Ableitung f´(x). Damit eine Funktion umkehrbar ist, muss die Ableitung f´(x) entweder immer positiv oder immer negativ sein. Manche Funktionen sind nur in bestimmten Teilbereichen umkehrbar, z. B. für 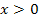 , dann muss die Ableitung zumindest in diesem Bereich immer das gleiche Vorzeichen haben.
, dann muss die Ableitung zumindest in diesem Bereich immer das gleiche Vorzeichen haben.

