Totale Wahrscheinlichkeit
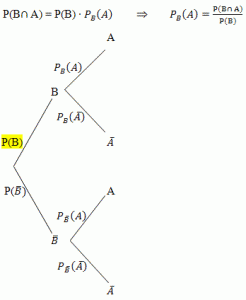
Unter einer totalen Wahrscheinlichkeit versteht man im Gegensatz zur bedingten Wahrscheinlichkeit eine Wahrscheinlichkeit, die keine Vorbedingung erfüllen muss. Die totale Wahrscheinlichkeit P(B) steht in einem Baumdiagramm, das mit den Verzweigungen B und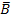 
beginnt, am vorderen Ast, der zu B führt. Vergleiche Baumdiagramm Nr.2!
Auch die Wahrscheinlichkeit P(A) ist eine totale Wahrscheinlichkeit. Die totalen Wahrscheinlichkeiten stehen in den Baumdiagrammen immer vorne, also an der ersten Verzweigung.
Baumdiagramm Nr.1
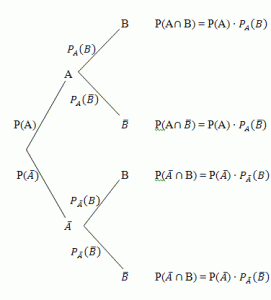
In einer häufig gestellten Aufgabe wird verlangt, aus den gegebenen Wahrscheinlichkeiten P(A),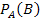 
und 
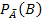die totale Wahrscheinlichkeit P(B) zu berechnen.
Mit Baumdiagramm Nr.1 ist das nicht schwer.
Vorgehensweise:
- Multipliziere nach der 1. Pfadregel die Wahrscheinlichkeiten am obersten Ast:
P(A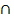 
B) = P(A)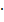 
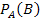
- Multipliziere nach der 1. Pfadregel die Wahrscheinlichkeiten am dritten Ast von oben:
P(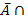 
B) = P( 
)
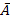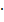
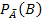
- Addiere diese beiden Werte und du erhältst P(B):
P(B) = P(A 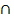B) + P( 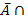B)
Diese Berechnung der totalen Wahrscheinlichkeit benötigst du auch oft bei der Berechnung von bedingten Wahrscheinlichkeiten. Mehr dazu im Bereich Stochastik im Kapitel Bedingte Wahrscheinlichkeit.
Baumdiagramm Nr.2
