Terrassenpunkt

Ein Terrassenpunkt ist ein Sonderfall des Wendepunktes, da es sich bei einem Terrassenpunkt um einen Wendepunkt mit waagrechter Tangente handelt. Damit an einer bestimmten Stelle ein Terrassenpunkt vorliegt, müssen folgende Bedingungen zugleich erfüllt sein:

f´( ) = 0        (waagrechte Tangente)

f´´(x) = 0         (Wendepunkt)

f´´´(x) 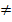0 oder Vorzeichenwechsel von f´´(x) an der Stelle (Nachweis des Wendepunktes)

Man erkennt einen Terrassenpunkt auch bereits bei der Monotonieuntersuchung der Funktion. Liegt an einer bestimmten Stelle eine waagrechte Tangente vor, d.h. es gilt f´( ) = 0, es ändert sich aber das Vorzeichen von f´(x) an dieser Stelle nicht, so liegt bei sicher ein Terrassenpunkt vor.

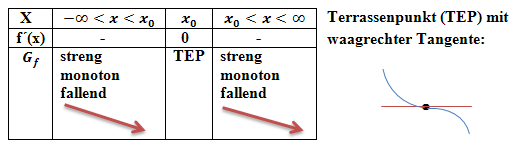
Monotonietabelle:

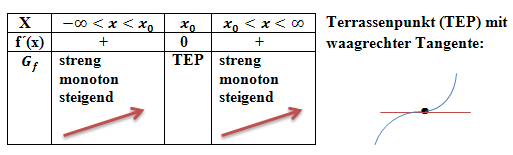
Oder:

Monotonietabelle:

Ein Terrassenpunkt liegt auch bei einer dreifachen Nullstelle vor. Siehe auch Vielfachheiten der Nullstellen!

Mehr rund um das Thema Terrassenpunkt findest du im Bereich Analysis in den Kapiteln Erste Ableitung f´(x) bzw. Zweite Ableitung f´´(x), sowie Monotonie und Extrema bzw. Kurvendiskussion.