Tangente

Unter einer Tangente versteht man eine Gerade, die einen Kreis oder einen Funktionsgraph in einem Punkt berührt.

Die Tangente an einen Kreis hat mit dem Kreis genau einen Punkt gemeinsam, sie schneidet den Kreis also nicht, sondern berührt ihn nur in einem Punkt, dem Berührpunkt. Unterscheide genau zwischen den Begriffen „berühren“ und „schneiden“! Eine Gerade, die den Kreis in zwei Punkten schneidet, ist daher keine Tangente, sondern eine Sekante. Die Tangente an einen Kreis steht immer senkrecht auf dem Radius.

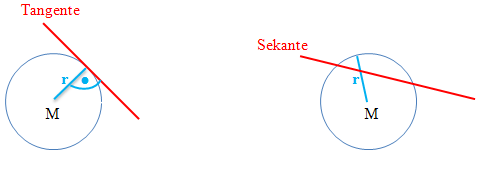
Die Tangente an den Graph einer Funktion berührt diesen ebenfalls, d.h. sie hat in der näheren Umgebung keinen weiteren gemeinsamen Punkt mit dem Graph. Sie kann jedoch eventuell weitere gemeinsame Punkte mit dem Graph an weiter entfernt liegenden Stellen haben. Die Steigung der Funktion entspricht dabei der Tangentensteigung in diesem Punkt. In der 11. Klasse des Gymnasiums und der FOS/ BOS (technischer Zweig) bzw. in der 12. Klasse der FOS/BOS (nicht-technische Zweige) lernst du, wie man die Tangentensteigung und somit die Steigung der Funktion in diesem Kurvenpunkt mit Hilfe der Differenzialrechnung, d.h. mit der Ableitung f´(x) berechnen kann.

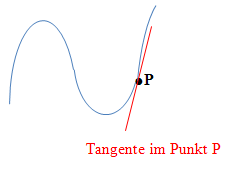
Von besonderem Interesse sind Punkte mit waagrechten Tangenten, also Punkte mit f´(x) = 0. Zu diesen Punkten zählen neben den Terrassenpunkten auch die Extrema (Minima und Maxima) einer Funktion. Um den Graph einer Funktion (ohne Wertetabelle) zeichnen zu können, benötigt man unter anderem diese Punkte. Daher werden sie, falls vorhanden, im Rahmen einer Kurvendiskussion berechnet.

In manchen Aufgaben wird auch die Gleichung der Tangente in einem bestimmten Kurvenpunkt P( | f( )) verlangt. Da eine Tangente eine Gerade ist, gilt für sie die allgemeine Geradengleichung y = mx + t. Zuerst berechnet man die Steigung m, indem man die x-Koordinate des Punktes P in die erste Ableitung f´(x) einsetzt.

m = f´( )

Danach kann der y-Achsenabschnitt t der Tangente ermittelt werden, indem man die Koordinaten von P und die soeben berechnete Steigung m in die allgemeine Geradengleichung y = mx + t einsetzt und nach t auflöst.

Eine andere Methode