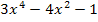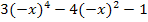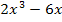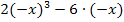Mathematische Begriffe und Definitionen » Symmetrie

Symmetrie

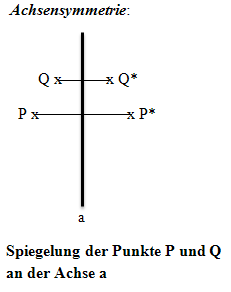
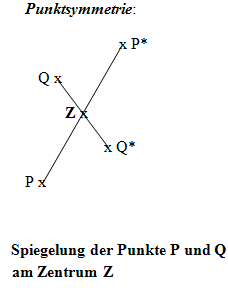
Man unterscheidet zwischen Achsen- und Punktsymmetrie. Bei der Achsensymmetrie wird ein einzelner Punkt oder eine ganze Figur an einer Gerade, der sogenannten Symmetrieachse, auch Spiegelachse genannt, gespiegelt. Bei der Punktsymmetrie wird an einem bestimmten Punkt, dem sogenannten Symmetriepunkt bzw. Zentrum, gespiegelt.

Symmetrische Figuren:

Sollst du überprüfen, ob eine gegebene Figur achsensymmetrisch ist, stellst du dir am besten die Frage, ob sich das Papier, welches die Figur enthält, so falten ließe, dass die eine Hälfte der Figur mit der anderen Hälfte zusammenfällt. Die Faltachse des Papiers entspricht der Symmetrie- bzw. Spiegelachse.

Manche Figuren haben nicht nur eine, sondern gleich mehrere Symmetrieachsen. Ein Rechteck besitzt beispielsweise zwei, ein Quadrat sogar vier Symmetrieachsen. Einen Extremfall stellt der Kreis dar:Er hat unendlich viele Symmetrieachsen, da jede Gerade, die durch den Mittelpunkt verläuft gleichzeitig Symmetrieachse des Kreises ist.

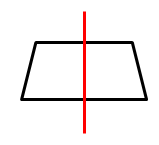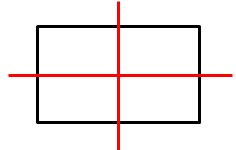
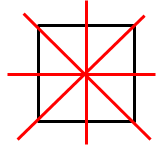
Abb.:Ein Rechteck, ein Quadrat und ein gleichschenkliges Trapez mit den jeweiligen Symmetrieachsen (rot eingezeichnet)

Manche Figuren sind gleichzeitig achsen- und punktsymmetrisch, andere sind dagegen entweder nur achsensymmetrisch oder nur punktsymmetrisch. Es gibt natürlich auch Figuren, die gar keine Symmetrie aufweisen. Ein Rechteck ist, genauso wie ein Quadrat, gleichzeitig achsen- und punktsymmetrisch. Die Symmetrieachsen sind in der Abbildung rot dargestellt, daher sind sie natürlich achsensymmetrisch. Der Schnittpunkt der Symmetrieachsen ist gleichzeitig aber auch Symmetriepunkt. Daher sind sie auch punktsymmetrisch. Ein gleichschenkliges Trapez (Vergleiche Abb. oben / rechte Figur!) ist dagegen nur achsensymmetrisch. Ein Symmetriepunkt existiert nicht. Ein Parallelogramm hat umgekehrt nur einen Symmetriepunkt (= Schnittpunkt der Diagonalen), aber keine Symmetrieachse! Es ist daher nur punktsymmetrisch.

Vorsicht:Viele Schüler halten die Diagonalen eines Parallelogramms für seine Symmetrieachsen. Das ist jedoch falsch! Um das zu verdeutlichen, hilft eine kleine Bastelarbeit:Zeichne dir auf ein einzelnes Blatt Papier ein beliebiges Parallelogramm ABCD, das jedoch keine Raute und kein Rechteck ist. (Das wären nämlich nur Sonderfälle, die tatsächlich wieder achsensymmetrisch wären.) Dieses Parallelogramm schneidest du nun aus und faltest es entlang einer der Diagonalen, z.B. AC. Du wirst sehen, dass der Eckpunkt B beim Zusammenfalten nicht mit dem Eckpunkt D zusammenfällt. Du kannst es auch mit anderen Faltachsen versuchen, doch es wird niemals klappen. Ein Parallelogramm ist eben nicht achsensymmetrisch!

Symmetrie bei Funktionen:

Auch bei Funktionen unterscheidet man zwischen achsen- und punktsymmetrischen Graphen. Hauptsächlich beschränkt man sich dabei auf die Symmetrie zum Koordinatensystem, d.h. auf die Achsensymmetrie zur y-Achse und die Punktsymmetrie zum Ursprung (= Nullpunkt). Natürlich kann eine Funktion auch zu einer anderen Achse oder zu einem anderen Punkt symmetrisch sein;das ist aber nur an Hand der Funktionsgleichung (bevor man den Graph gezeichnet hat) nicht so einfach zu erkennen.

Den rechnerischen Nachweis einer Symmetrie musst du vor der Oberstufe noch nicht können. Auf die rechnerische Untersuchung des Symmetrieverhaltens wird erst in der 11. Klasse im Rahmen der Kurvendiskussion eingegangen.

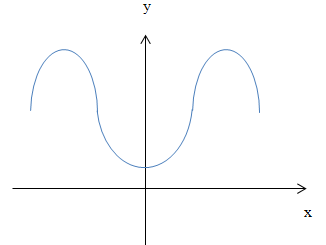
Abb.:Graph einer zur y-Achse symmetrischen Funktion

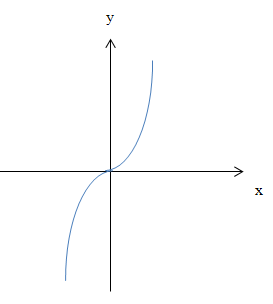
Abb.:Graph einer zum Ursprung punktsymmetrischen Funktion

Symmetrie zum Koordinatensystem rechnerisch nachweisen:

f(-x) = f(x)

Achsensymmetrie zur y-Achse

(z.B.:Funktionen, die nur gerade

x-Potenzen haben)

f(-x) = – f(x)

Punktsymmetrie zum Ursprung

(z.B.:Funktionen, die nur ungerade

x- Potenzen haben)

Bsp.:

f(x) =

f(-x) =

f(-x) = = f(x)