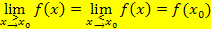Stetigkeit
Ist eine Funktion stetig, lässt sich ihr Graph (zumindest innerhalb ihrer Definitionsmenge) zeichnen, ohne den Stift abzusetzen. Der Graph einer stetigen Funktion hat für x 
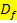 keine Sprungstellen. Knicke bzw. Spitzen kann er jedoch haben.
keine Sprungstellen. Knicke bzw. Spitzen kann er jedoch haben.
Vorsicht:Die Regel, dass eine Funktion nicht stetig ist, wenn sie eine oder mehrere Sprungstellen hat, gilt wirklich nur an Stellen innerhalb der Definitionsmenge! Liegt eine Sprungstelle an einer Definitionslücke, ist die Funktion dennoch stetig! Betrachte dazu auch das letzte der unten gezeigten Beispiele!
Bitte jetzt nicht erschrecken! Die folgende Definition ist leider kompliziert, wird aber gleich danach noch erklärt.
Definition: Eine Funktion f(x) ist an der Stelle 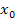  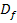 stetig, wenn gilt: stetig, wenn gilt:
|
Anmerkung:
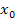 ist eine konkrete Zahl. Eine Funktion wird immer lokal, also an einer bestimmten Stelle
ist eine konkrete Zahl. Eine Funktion wird immer lokal, also an einer bestimmten Stelle 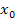 auf Stetigkeit untersucht. Im ersten nachfolgenden Beispiel (siehe unten) ist
auf Stetigkeit untersucht. Im ersten nachfolgenden Beispiel (siehe unten) ist  . Mit
. Mit 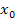 ist also die x-Koordinate der zu untersuchende „Problemstelle“ gemeint, an der die jeweiligen Teilfunktionen einer teilweise definierten Funktion zusammenstoßen.
ist also die x-Koordinate der zu untersuchende „Problemstelle“ gemeint, an der die jeweiligen Teilfunktionen einer teilweise definierten Funktion zusammenstoßen.
 Sprich:„Limes von x gegen
Sprich:„Limes von x gegen 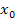 von rechts der Funktion f von x“
von rechts der Funktion f von x“
Das Größer-Zeichen über dem Pfeil zwischen x und 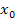 bedeutet:Annäherung an die Stelle
bedeutet:Annäherung an die Stelle 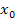 von rechts. x ist also ein klein wenig größer als der feste Zahlenwert
von rechts. x ist also ein klein wenig größer als der feste Zahlenwert 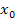 . Man nähert sich daher von rechts an die „Problemstelle“
. Man nähert sich daher von rechts an die „Problemstelle“ 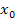 an.
an.
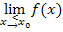 Sprich:„Limes von x gegen
Sprich:„Limes von x gegen 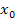 von links der Funktion f von x“
von links der Funktion f von x“
Das Kleiner-Zeichen über dem Pfeil zwischen x und 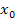 bedeutet:Annäherung an die Stelle
bedeutet:Annäherung an die Stelle 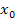 von links. x ist also etwas kleiner als der feste Zahlenwert
von links. x ist also etwas kleiner als der feste Zahlenwert 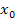 . Man nähert sich daher von links an die „Problemstelle“
. Man nähert sich daher von links an die „Problemstelle“ 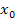 an.
an.
Oben gezeigte Definition noch einmal in Worten:Ist das Ergebnis des Limes von rechts gleich dem Limes von links und stimmt dieses Ergebnis auch mit dem Funktionswert an der Stelle 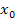

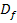 überein, ist die Funktion an der Stelle
überein, ist die Funktion an der Stelle 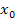 stetig, d.h. sie hat dort keine Sprungstelle.
stetig, d.h. sie hat dort keine Sprungstelle.
Anschaulich bedeutet das:Wenn man auf dem Graphen der Funktion f mit dem rechten Zeigefinger von rechts und zugleich mit dem linken Zeigefinger von links an die Stelle 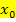 herangeht, und es treffen sich die Fingerspitzen, dann ist die Funktion f an der Stelle
herangeht, und es treffen sich die Fingerspitzen, dann ist die Funktion f an der Stelle 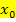 stetig.
stetig.
Beispiele:![]()


Hauptsächlich bei teilweise definierten Funktionen (= aus mehreren Teilfunktionen zusammengesetzte Funktionen, oft mit geschweifter Klammer geschrieben) wird ab der 11. Klasse die rechnerische Überprüfung der Stetigkeit verlangt. Dies kann entweder mit Hilfe der h-Methode oder wesentlich einfacher durch bloßes Einsetzen des Wertes 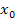 in die jeweiligen Teilfunktionsgleichungen geschehen. Ergibt sich dabei immer das gleiche Ergebnis, d.h. der Limes von links, der Limes von rechts und der Funktionswert sind an dieser Stelle gleich, ist die Funktion dort stetig.
in die jeweiligen Teilfunktionsgleichungen geschehen. Ergibt sich dabei immer das gleiche Ergebnis, d.h. der Limes von links, der Limes von rechts und der Funktionswert sind an dieser Stelle gleich, ist die Funktion dort stetig.
Beispiel: f(x) = 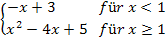
Die beiden Teilfunktionen y = 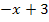 und y =
und y = 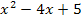 stoßen an der Stelle
stoßen an der Stelle  zusammen, da die eine für
zusammen, da die eine für  und die andere für
und die andere für 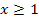 gilt. Daher muss die Stetigkeit an der Stelle
gilt. Daher muss die Stetigkeit an der Stelle  überprüft werden. Es soll auf die h-Methode verzichtet werden.
überprüft werden. Es soll auf die h-Methode verzichtet werden.
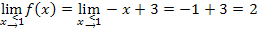

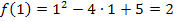
Es ergibt sich jedes Mal das selbe Ergebnis. Daher ist die Funktion f bei  stetig.
stetig.
Weitere Beispiele zur rechnerischen Überprüfung der Stetigkeit (auch mit der h-Methode) und ausführlichere Erläuterungen zu diesem Thema findest du im Bereich Analysis im Kapitel Stetigkeit und Differenzierbarkeit.