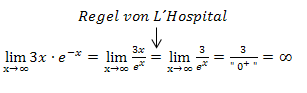Regel von L´Hospital
Die Regel von L´Hospital ist eine Regel zur Berechnung von Grenzwerten, die zu Ausdrücken der Form 
oder 
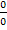führen, sogenannte Unbestimmte Ausdrücke.
Die Regel von L´Hospital besagt im Prinzip Folgendes:
Bei Grenzwerten, die (vom Vorzeichen abgesehen) zu Ausdrücken der Form oder 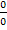führen, gilt: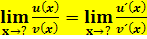 
Das bedeutet, dass man Grenzwerte der Form 
oder 
berechnen kann, indem man den Zähler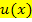 
und den Nenner 
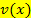der vorliegenden Funktion 
getrennt ableitet (also nicht mit der Quotientenregel) und dann den entsprechenden Grenzwert von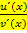 
berechnet.
Wie man jeweils die Ableitung von Zähler und Nenner bildet, wird ausführlich erklärt im Kapitel Differenzialrechnung bei Einfache Ableitungsregelnund Weitere Ableitungsregeln.
Beispiel für die Berechnung eines Grenzwertes mit der Regel von L´Hospital:
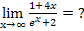
Für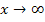 
geht sowohl der Zähler gegen 
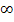als auch der Nenner. Es ergibt sich damit ein Ausdruck der Form .
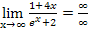
Die Frage ist nun, ob der Zähler oder der Nenner stärker gegen Unendlich geht. Wer wächst schneller? Die Funktion mit der größeren Steigung geht auch schneller gegen Unendlich. Daher darf man den Grenzwert der Ableitungen von Zähler bzw. Nenner an Stelle des ursprünglichen Grenzwertes berechnen. (Die Ableitung entspricht bekanntlich der Steigung der Funktion.) D.h. wir wenden die Regel von L´Hospital an.
Manche Grenzwerte lassen sich auch erst nach mehrmaliger Anwendung der Regel von L´Hospital berechnen. Dann leitet man einfach so oft Zähler und Nenner jeweils getrennt ab, bis sich nicht mehr oder 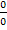ergibt. Man darf die Regel von L´Hospital also so oft hintereinander anwenden bis sich kein unbestimmter Ausdruck mehr ergibt und man den Grenzwert ausrechnen kann.
Beispiel für die dreimalige Anwendung der Regel von L´Hospital:
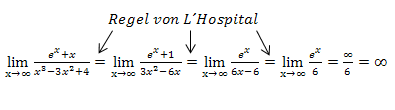
Die Regel von L´Hospital hilft auch Grenzwerte zu lösen, die zu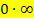 
oder 
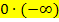führen. Dabei kann man nämlich ebenfalls nicht allgemein sagen, was herauskommt. Auch 
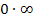und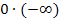 
sind unbestimmte Ausdrücke ebenso wie oder 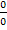. Es kommt wieder darauf an, welcher der beiden Faktoren überwiegt. Bei Grenzwerten mit 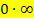oder 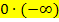muss jedoch vorweg die Funktion in einen Bruch umgeformt werden;das geht am besten, indem einer der beiden Faktoren des Produkts in den Nenner des Bruchs geschrieben und gleichzeitig das Vorzeichen des Exponenten dieses Faktors umgedreht wird. Man kann aber auch stattdessen einfach den Kehrwert dieses Faktors in den Nenner schreiben. Erst danach kann die Regel von L´Hospital angewendet werden.
Beispiel für die Anwendung der Regel von L´Hospital bei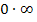 
:
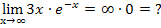
Umwandlung von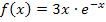 
in einen Bruch:
Es bietet sich hier an, den Faktor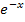 
in den Nenner des Bruchs zu verschieben, indem man das Vorzeichen des Exponenten umdreht.
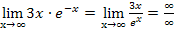
Nun kann die Regel von L´Hospital angewendet werden:
