R^2 (Zweidimensionales Koordinatensystem)
Es handelt sich beim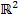 
um ein Koordinatensystem mit zwei Achsen, die meist als x- und y-Achse bezeichnet werden. In der analytischen Geometrie (= Vektorgeometrie) finden sich aber auch die Bezeichnungen 
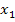– und 
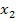-Achse.
Sowohl für x als auch für y sind alle reellen Zahlen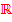 
zugelassen. Mathematisch gesagt:x ist ein Element der Menge 
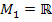, y ist ein Element der Menge 
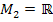. Die Produktmenge 
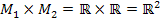beschreibt daher die Menge aller Punkte P(x│y) im zweidimensionalen Koordinatensystem.
Wenn du bei einer Aufgabe die Angabe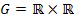 
oder 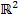findest, bedeutet das nur, dass du mit einem ganz normalen x, y-Koordinatensystem arbeiten sollst. Es handelt sich um eine Aufgabe in der Ebene und nicht im Raum!
Für alle Realschüler ist das sowieso das einzig bekannte Koordinatensystem;die Angabe 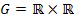bei den Realschul-Abschlussprüfungen kannst du insofern übergehen. Erst für Schüler der gymnasialen Oberstufe kommt der Angabe 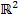eine größere Bedeutung zu:Beispielsweise bei der Überprüfung der Lagebeziehungen zweier Geraden. Im 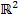, also im zweidimensionalen Koordinatensystem können sich zwei Geraden schneiden, sie können echt parallel oder identisch sein. Im 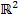können die beiden Geraden nicht windschief zueinander sein! (Anmerkung:Windschief sind Geraden, die nicht parallel sind, die sich aber auch nicht schneiden; sie laufen also „schräg“ im Raum aneinander vorbei.) Windschief können Geraden nur im dreidimensionalen Koordinatensystem, also im Raum, d.h. im 
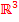, sein!
