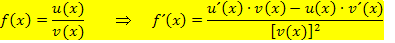Quotientenregel
Wenn man die Ableitungeines Quotienten bilden soll, der im Nenner die Variable (meist x genannt) enthält, braucht man die Quotientenregel. Die Quotientenregel ist also eine Ableitungsregel für Brüche mit der Variablen im Nenner. Wenn die Variable wie üblich mit x bezeichnet wird, kann man folgendes sagen:Die Quotientenregel muss angewendet werden, wenn die Ableitung einer Funktion gesucht ist, die x im Nenner enthält. Ob x auch im Zähler der Funktion vorkommt, ist egal.
| Willst du einen Bruch (mit x im Nenner) ableiten, gehst du folgendermaßen vor:
Zähler ableiten mal den Nenner hinschreiben minus Zähler hinschreiben mal Nenner ableiten und das Ganze durch das Quadrat des Nenners (abgeschrieben) dividieren. In mathematischer Form sieht die Quotientenregel so aus:
|
Bei Brüchen darf man also nicht einfach Zähler und Nenner getrennt ableiten, wenn man die Ableitung des gesamten Bruchs sucht!
Manche Lehrer verwenden auch die folgende Form der Quotientenregel:
N steht für den Nenner der Funktion;Z für den Zähler. Mit AZ ist die Ableitung des Zählers gemeint;mit AN die Ableitung des Nenners.
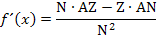
Sprich:„NAZ minus ZA(H)N durch N Quadrat“
Der Spruch ist recht einprägsam, hat aber einen großen Nachteil. Es ist nicht eindeutig klar, was NAZ bzw. ZAN bedeutet. NAZ könnte nämlich auch fälschlicherweise für „Nennerableitung mal Zähler“ gehalten werden. (Korrekt ist ja „Nenner mal Ableitung des Zählers“.) Das gleiche Problem tritt bei ZAN auf. Ist das jetzt „Zählerableitung mal Nenner“ oder „Zähler mal Ableitung des Nenners“? (Korrekt ist die letztere Variante.) Du solltest die „NAZ minus ZAN“-Form der Quotientenregel wirklich nur dann anwenden, wenn dir hundertprozentig klar ist, wie das gemeint ist. Sonst besser in die Formelsammlung / Merkhilfe schauen;dort steht die Quotientenregel mit u und v. Da kann man nichts verwechseln.
Konkrete Aufgabenbeispiele zur Quotientenregel mit ausführlichen Lösungen findest du im Kapitel Einführung in die Differenzialrechnung bei Weitere Ableitungsregeln.