Primfaktorzerlegung
Wenn eine Zahl ausschließlich als Produkt von Primzahlen oder ihrer Potenzen geschrieben wird, spricht man von einer Primfaktorzerlegung.
Beispiel der Primfaktorzerlegung der Zahl 18:
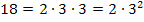
Vorgehensweise bei der Primfaktorzerlegung einer gegebenen Zahl:
Als erstes überlegt man sich zwei beliebige Zahlen, die miteinander multipliziert die Zahl ergeben. Diese zwei Zahlen müssen noch keine Primzahlen sein. Nun zerlegt man jede der beiden Zahlen so lange weiter, bis nur noch Primzahlen in dem Produkt vorkommen.
Bsp.: Zerlege die Zahl 450 in ihre Primfaktoren!
Lösung:
Wir überlegen uns zwei Zahlen, deren Produkt 450 ist. Da die Zahl 450 auf 0 endet, ist sie sicher durch 10 teilbar. Man erkennt leicht:
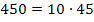
Weder die Zahl 10, noch die Zahl 45 sind Primzahlen. Wir müssen also beide noch weiter zerlegen, solange bis das Produkt nur noch aus Primzahlen besteht. Statt der Zahl 10 schreiben wir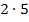 
und statt der Zahl 45 schreiben wir beispielsweise 
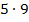. Die Zahl 9 ist noch keine Primzahl, sie muss noch einmal zerlegt werden, nämlich in 
.
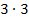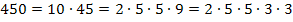
Jetzt ist die Zahl 450 in ihre Primfaktoren zerlegt. Wir ordnen die Primzahlen noch in aufsteigender Reihenfolge und schreiben dann alles so weit möglich mit Potenzen. (Die Potenzschreibweise muss nicht unbedingt verwendet werden, ist jedoch übersichtlicher.)
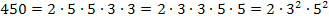
Fertig!
Die Primfaktorzerlegung ist vor allem bei der Ermittlung eines gemeinsamen Nenners mehrerer Brüche manchmal sehr hilfreich. Mehr dazu bei Hauptnenner.
