Polynomdivision

Um ein Polynomdurch ein anderes Polynom zu dividieren, verwendet man die sogenannte Polynomdivision.

Um beispielsweise den Ausdruck 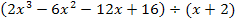auszurechnen, wird die Polynomdivision angewendet. Das geht so ähnlich wie bei der normalen Division von Zahlen mit Nebenrechnung auf dem Papier, die du in der Grundschule gelernt hast. Wie auch bei der Division normaler Zahlen, gibt es Polynomdivisionen, die aufgehen, und welche, bei denen ein Rest übrig bleibt, die also nicht aufgehen.

Wie kann man im Voraus beurteilen, ob eine Polynomdivision aufgehen wird? ·         Setzte den Ausdruck, der hinter dem Geteilt-Zeichen steht, gleich Null. ·         Löse diese Gleichung nach x auf. ·         Setze das Ergebnis (bzw. die einzelnen Ergebnisse) in den Ausdruck ein, der bei der Polynomdivision vor dem Geteilt-Zeichen steht. ·         Kommt dabei (bei jedem Ergebnis) Null heraus, dann geht die Polynomdivision sicher auf. Andernfalls geht sie nicht auf;es wird ein Rest bleiben.

Probieren wir das doch gleich mal an unserem Beispiel aus.

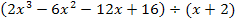
Aus 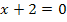ergibt sich offensichtlich 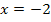. Das setzen wir jetzt in die vordere Klammer, also 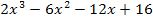in ein:

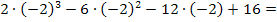
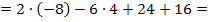
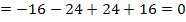
Es ergibt sich die Zahl 0;die Polynomdivision muss aufgehen. Wenn du dich jetzt fragst, warum das so ist, dann lies bitte weiter;später werden wir noch einmal darauf zurückkommen.

Wie funktioniert denn nun eine Polynomdivision?

Jetzt werden wir die Polynomdivision aus unserem Beispiel endlich durchführen;daran wird das Prinzip erklärt.

Bevor du eine Polynomdivision beginnst, musst du auf Folgendes achten:

Sowohl in der vorderen Klammer, als auch in der hinteren müssen alle Potenzen von x in absteigender Reihenfolge angeordnet sein. Wenn das nicht der Fall, unbedingt selbst ordnen! In unserem Beispiel passt schon alles. Außerdem fehlt auch keine Potenz von x, wir können direkt mit der Polynomdivision beginnen.

Wichtig:Wenn du einmal eine Polynomdivision durchführen musst, bei der eine oder mehrere Potenzen der Variablen fehlen, solltest du unbedingt die fehlende Potenz mit dem Koeffizienten 0 ergänzen! (Der Koeffizient ist die Zahl davor.)

Zum Beispiel: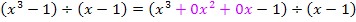

Jetzt aber wieder zurück zu unserem Einführungsbeispiel:

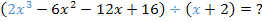
Wir müssen mit denjenigen Ausdrücken beginnen, die jeweils ganz vorne in den beiden Klammern stehen;sie sind hier blau geschrieben. Damit es dir leichter fällt, die folgenden Einzelschritte nachzuvollziehen, sind diejenigen Teile, welche du jeweils in einem bestimmten Schritt ausrechnen musst, in Blau geschrieben. Das jeweilige Ergebnis dieses Rechenschrittes ist in Grün geschrieben.

Als erstes überlegst du dir, was 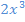geteilt durch 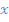ergibt. Oder du stellst dir andersherum die Frage, mit was man 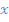multiplizieren muss, um auf 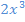zu kommen. Das ist letztendlich dasselbe. Überlege dir das gleich ´mal alleine!

Du solltest 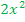als Ergebnis erhalten haben. 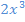geteilt durch x ergibt schließlich .

---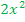