Polynom
Mit einem Polynom, auch ganzrationale Funktion genannt, ist eine Funktion f(x) mit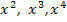 
oder noch höheren Potenzen von x gemeint;x darf aber in der Funktionsgleichung nur mit natürlichen (d.h. ganzen, positiven) Zahlen als Exponenten vorkommen. Daher steht bei einem Polynom, einer ganzrationalen Funktion, x niemals im Nenner, denn 
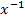ist ja nur eine andere Schreibweise für 
und das ist eine gebrochenrationale Funktion und keine ganzrationale.
Den höchsten vorkommenden Exponenten von x bezeichnet man als Grad des Polynoms. Am Grad des Polynoms lässt sich bereits erkennen, wie viele Nullstellen die Funktion höchstens haben kann. Ein Polynom n-ten Grades hat immer höchstens n Nullstellen. Auch über den Verlauf des Graphen können nur mit Hilfe des Grades des Polynoms bereits einige wichtige Aussagen gemacht werden.
Beispiel für ein Polynom dritten Grades: f(x) = 
Beispiel für ein Polynom vierten Grades: f(x) =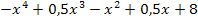 
Wie in den beiden Beispielen zu erkennen ist, sind die Potenzen von x nach absteigenden Exponenten geordnet.
Allgemein schreibt man ein Polynom n-ten Grades folgendermaßen:
f(x) =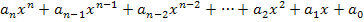 
mit n 
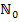
Statt den etwas erschreckenden Bezeichnungen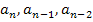 
… können für die Koeffizienten (=Zahlen vor den Potenzen von x) auch die Buchstaben a, b, c … verwendet werden. Dadurch sieht die ganze Sache schon nicht mehr ganz so kompliziert aus.
Beispielsweise kann ein Polynom dritten Grades allgemein in den beiden folgenden Formen geschrieben werden: f(x) =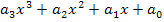 
oder: f(x) =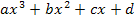 
Die hintere Schreibweise ist wohl etwas „angenehmer“ und wird daher auf dieser website hauptsächlich verwendet werden. Die andere Schreibweise hat jedoch auch ihre Berechtigung. So lässt beispielsweise die Bezeichnung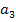 
eindeutig darauf schließen, dass es sich um den Koeffizienten von 
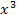handelt, also um die Zahl, die vor 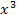steht, und nicht etwa vor einer anderen x-Potenz.
Mehr zum Thema Polynome findest du im Bereich Analysis in den folgenden Kapiteln:
Nullstellen von ganzrationalen Funktionen (Polynome dritten und höheren Grades) wichtig für Schüler der 10. Klasse Gymnasium und 11. Klasse FOS und BOS (Abiturstoff!)
Polynomfunktionen / Ganzrationale Funktionen (Kurvendiskussion)
