Monotonie/Monotonieverhalten

Unter der Monotonie oder dem Monotonieverhalten einer Funktion versteht man das Steigungsverhalten der Funktion. Die Untersuchung der Monotonie einer Funktion ist ein Teil der sogenannten Kurvendiskussion, welche ab der 11. Klasse auf dem Lehrplan des Gymnasiums und der FOS bzw. BOS steht. Gut darstellen lässt sich die Monotonie in Tabellenform, in einer sogenannten Monotonietabelle.

Beispiel einer Monotonietabelle:

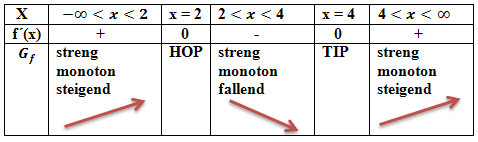
Manche Lehrer stellen das Steigungsverhalten nicht in Tabellenform dar, sondern in folgender Art und Weise:

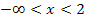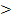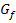für  :       f´(x) 0          streng monoton steigend

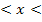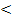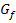für      2 4:       f´(x) 0          streng monoton fallend

für      4 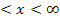:      f´(x) 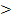0  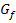        streng monoton steigend

In dieser Form lässt sich jedoch nicht so gut erkennen, welche Art von Extremum vorliegt, also ob es sich bei dem Punkt mit waagrechter Tangente jeweils um einen Tiefpunkt oder um einen Hochpunkt handelt. Daher ist an sich die Monotonietabelle zu bevorzugen.

Bevor die Monotonietabelle angelegt werden kann, müssen jedoch zuerst die x-Koordinaten der Punkte mit waagrechten Tangenten ermittelt werden. (In der oben als Beispiel dargestellten Monotonietabelle x = 2 und x = 4) Das macht man mit dem Ansatz f´(x) = 0, da die Steigung f´(x) der Funktion gleich der Tangentensteigung in diesem Punkt, also gleich Null sein muss. Zur Berechnung der Steigung einer Funktion f(x) benötigt man daher die erste Ableitung f´(x).

Mit Hilfe des Steigungsverhaltens, d.h. der Monotonie, kann leicht gezeigt werden, dass ein Extremum und kein Terrassenpunkt vorliegt. Nur bei einem Vorzeichenwechsel von f´(x) liegt ein Extremum vor.

Die Untersuchung der Monotonie dient außerdem der Unterscheidung zwischen relativen Hochpunkten(Maxima) und relativen Tiefpunkten (Minima). Besonders gut lässt sich die Art des Extremums aus der Monotonietabelle ablesen. Mehr dazu im Bereich Analysis bei Relationen und Funktionen im Kapitel Monotonie und Extrema.