Mächtigkeit des Ergebnisraums |Ω|

Unter der Mächtigkeit des Ergebnisraums 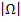, auch Betrag von 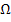(sprich „Omega“) genannt, versteht man die Anzahl aller möglichen Fälle, genauer gesagt die Anzahl aller möglichen Elementarereignisse.

Beispiele:

Einmaliges Werfen eines Würfels

Der Würfel kann die Augenzahlen 1, 2, 3, 4, 5 oder 6 zeigen. Deshalb lautet der Ergebnisraum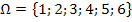

Es gibt 6 verschiedene Elementarereignisse, d.h. 6 verschiedene Möglichkeiten. Daher gilt für die Mächtigkeit des Ergebnisraums:

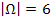
Zweimaliges Werfen einer Münze (unter Beachtung der Reihenfolge)

Auf der einen Seite der Münze ist ein Wappen W, auf der anderen Seite eine Zahl Z. Wird diese Münze zweimal nacheinander geworfen, gibt es die folgenden verschiedenen Fälle:

Zweimal Wappen WW

Zuerst Wappen, dann Zahl WZ

Zuerst Zahl, dann Wappen ZW

Zweimal Zahl ZZ

Daher lautet der Ergebnisraum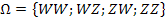

Es gibt also 4 Elementarereignisse, d.h. 4 verschiedene mögliche Fälle. Daher gilt für die Mächtigkeit des Ergebnisraums:

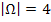
Um etwas größere Ergebnisräume zu ermitteln, zeichnet man sich oft auch ein sogenanntes Baumdiagrammund liest daraus alle möglichen Elementarereignisse ab. Mit Hilfe der Kombinatorik kann die Mächtigkeit eines Zufallsexperiments direkt berechnet werden, ohne vorher den Ergebnisraum anzugeben. Das ist vor allem wichtig für die Berechnung von Laplace-Wahrscheinlichkeiten.