Linearkombination
Mit dem Begriff „Linearkombination“ ist in der analytischen Geometrie gemeint, dass ein Vektor als Summe der Vielfachen zweier oder mehrerer anderer Vektoren dargestellt werden kann. Das ist zwar eine schöne mathematische Erklärung, doch wahrscheinlich sagt dir dieser Satz nicht wirklich viel. Also schauen wir uns doch einfach ein konkretes Beispiel einer Linearkombination an:
Betrachte die rechts dargestellten Vektoren 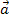 ,
, 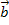 und
und  !
!
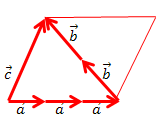
Die drei Vektoren sollen gemeinsam in einer Ebene liegen, welche in der Zeichnung als Parallelogramm angedeutet ist. Der Vektor  lässt sich daher als Linearkombination der Vektoren
lässt sich daher als Linearkombination der Vektoren 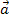 und
und 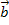 ausdrücken.
ausdrücken.
In diesem Beispiel lässt sich offensichtlich folgende Linearkombination bilden:
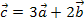
Der Vektor  lässt sich also als Summe des Dreifachen von
lässt sich also als Summe des Dreifachen von 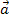 und des Doppelten von
und des Doppelten von 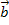 darstellen. Der Vektor
darstellen. Der Vektor  lässt sich also als Summe der Vielfachen zweier anderer Vektoren darstellen. Hätten sich die drei Vektoren nicht gemeinsam in einer Ebene befunden, wäre es nicht möglich gewesen
lässt sich also als Summe der Vielfachen zweier anderer Vektoren darstellen. Hätten sich die drei Vektoren nicht gemeinsam in einer Ebene befunden, wäre es nicht möglich gewesen  als Linearkombination der Vektoren
als Linearkombination der Vektoren 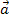 und
und 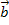 auszudrücken. Es ist somit nur dann möglich eine Linearkombination der Vektoren
auszudrücken. Es ist somit nur dann möglich eine Linearkombination der Vektoren 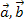 und
und  zu bilden, wenn sie in einer gemeinsamen Ebene liegen, oder zumindest in eine Ebene verschoben werden können. Dann sagt man, die drei Vektoren sind linear abhängig oder komplanar. Mehr dazu im Kapitel Lineare Abhängigkeit von Vektoren.
zu bilden, wenn sie in einer gemeinsamen Ebene liegen, oder zumindest in eine Ebene verschoben werden können. Dann sagt man, die drei Vektoren sind linear abhängig oder komplanar. Mehr dazu im Kapitel Lineare Abhängigkeit von Vektoren.
Wie wird nun eine Linearkombination allgemein geschrieben? Das hängt davon ab, wie viele Vektoren beteiligt sind.
Auf die folgende Art und Weise wird beispielsweise ein Vektor  allgemein als Linearkombination der zwei Vektoren
allgemein als Linearkombination der zwei Vektoren 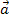 und
und 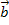 ausgedrückt:
ausgedrückt:
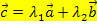
![]()
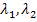
 ℝ
ℝ
Es gibt aber auch Linearkombinationen aus drei oder mehr Vektoren. So kann beispielsweise ein Vektor 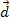 als Linearkombination der drei Vektoren
als Linearkombination der drei Vektoren 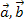 und
und  dargestellt werden:
dargestellt werden:
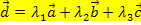
![]()
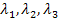
 ℝ
ℝ
Dies ist jedoch nur dann möglich, wenn entweder die drei Vektoren 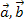 und
und  linear unabhängig sind oder wenn alle vier Vektoren
linear unabhängig sind oder wenn alle vier Vektoren 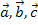 und
und 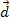 in einer gemeinsamen Ebene liegen bzw. in eine Ebene hinein verschoben werden könnten.
in einer gemeinsamen Ebene liegen bzw. in eine Ebene hinein verschoben werden könnten.
Wie berechnet man nun aber die Werte 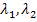 und bei einer Linearkombination aus drei Vektoren
und bei einer Linearkombination aus drei Vektoren 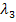 ? Schauen wir uns doch einfach jeweils ein konkretes Beispiel für die Berechnung einer Linearkombination mit zwei bzw. drei Vektoren an:
? Schauen wir uns doch einfach jeweils ein konkretes Beispiel für die Berechnung einer Linearkombination mit zwei bzw. drei Vektoren an:
1. Bsp.:
Stelle 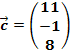 als Linearkombination der Vektoren
als Linearkombination der Vektoren 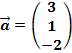 und
und 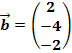 dar!
dar!
Lösung:
Allgemeiner Ansatz: 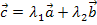
Wir setzen die gegeben Vektoren in den allgemeinen Ansatz ein:
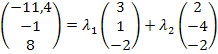
Nun wird jede Zeile als einzelne Gleichung aufgefasst. So erhält man ein Gleichungssystem aus drei Gleichungen mit den zwei Unbekannten 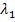 und
und 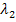 .
.
I 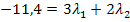
II 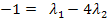
III 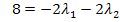
Es handelt sich hierbei um ein überbestimmtes Gleichungssystem, d.h. wir mehr Gleichungen als Unbekannte. Genauer gesagt, gibt es eine Gleichung zu viel. Wir lösen das Gleichungssystem am besten, indem wir eine Gleichung, beispielsweise Gleichung I, vorerst weglassen, mit den verbleibenden Gleichungen 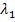 und
und 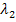 berechnen und danach die Ergebnisse jeweils in die zuerst weggelassene Gleichung zur Kontrolle einsetzen. Ergibt sich dabei eine wahre Aussage, lässt sich
berechnen und danach die Ergebnisse jeweils in die zuerst weggelassene Gleichung zur Kontrolle einsetzen. Ergibt sich dabei eine wahre Aussage, lässt sich  tatsächlich als Linearkombination der Vektoren
tatsächlich als Linearkombination der Vektoren 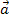 und
und 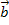 darstellen. Die drei Vektoren liegen dann in einer gemeinsamen Ebene. Ergibt sich bei der Kontrolle dagegen ein Widerspruch, sind die drei Vektoren linear unabhängig, d.h. sie spannen einen Raum auf, und es lässt sich keine Linearkombination bilden. Versuche doch gleich selbst mit den Gleichungen II und III die Unbekannten
darstellen. Die drei Vektoren liegen dann in einer gemeinsamen Ebene. Ergibt sich bei der Kontrolle dagegen ein Widerspruch, sind die drei Vektoren linear unabhängig, d.h. sie spannen einen Raum auf, und es lässt sich keine Linearkombination bilden. Versuche doch gleich selbst mit den Gleichungen II und III die Unbekannten 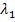 und
und 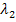 zu berechnen, ohne vorher die folgende Lösung anzuschauen!
zu berechnen, ohne vorher die folgende Lösung anzuschauen!
Gleichung I lassen wir vorerst weg. Hier noch einmal die anderen beiden Gleichungen:
II 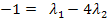
III 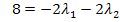
Du kannst nun entweder das Additions- oder das Einsetzungsverfahren anwenden. Vermutlich bevorzugst du das Einsetzungsverfahren. Daher wird im Folgenden diese Methode gezeigt. Gleichung II lässt sich leicht nach 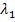 auflösen.
auflösen.
II 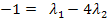 |
| 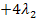
![]()
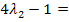
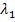
II´ 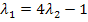
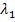 in III
in III 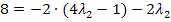
![]()
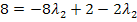
![]()
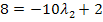 |
| 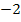
![]()
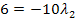
![]() |
| 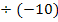
![]()
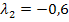
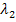 in II´
in II´ 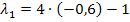
![]()
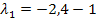
![]()
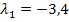
Kontrolle:
Um festzustellen, ob überhaupt eine Linearkombination existiert, müssen wir 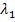 und
und 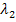 in die vorher weggelassene Gleichung I einsetzen und überprüfen, ob sich eine wahre Aussage ergibt.
in die vorher weggelassene Gleichung I einsetzen und überprüfen, ob sich eine wahre Aussage ergibt.
Hier noch einmal die Gleichung I: 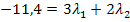
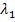 und
und 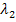 in I
in I![]()
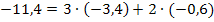
![]()
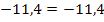 (wahr)
(wahr)
Es gibt also eine Linearkombination. Um sie zu erhalten, muss man nur noch die berechneten Werte für 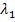 und
und 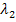 in den allgemeinen Ansatz
in den allgemeinen Ansatz 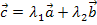 einsetzen. So erhält man:
einsetzen. So erhält man:
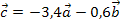
Fertig!
2. Bsp.:
Stelle 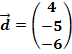 als Linearkombination der Vektoren
als Linearkombination der Vektoren 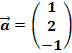 ,
, 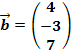 und
und 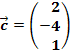 dar!
dar!
Lösung:
Allgemeiner Ansatz: 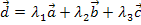
Wir setzen die gegeben Vektoren in den allgemeinen Ansatz ein:
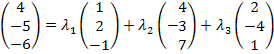
Nun wird jede Zeile als einzelne Gleichung aufgefasst. So erhält man ein Gleichungssystem aus drei Gleichungen mit den drei Unbekannten 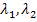 und
und 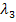 .
.
I 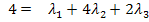
II 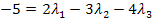
III 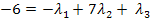
Nun liegt ein Gleichungssystem mit drei Gleichungen und drei Unbekannten vor. Wir lösen es mit dem Gauß-Algorithmus. (Das ist eigentlich nur ein verfeinertes Additionsverfahren. Gleichung I lassen wir stehen, aus Gleichung II und III wird zuerst jeweils 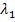 eliminiert. Um aus Gleichung II die Unbekannte
eliminiert. Um aus Gleichung II die Unbekannte 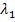 zu eliminieren, nehmen wir I und II. Die Gleichung I wird dann mit 2 multipliziert und II davon abgezogen. Dadurch fällt die Unbekannte
zu eliminieren, nehmen wir I und II. Die Gleichung I wird dann mit 2 multipliziert und II davon abgezogen. Dadurch fällt die Unbekannte 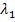 heraus. Die so entstandene Gleichung nennen wir II´. Um aus Gleichung III ebenfalls die Unbekannte
heraus. Die so entstandene Gleichung nennen wir II´. Um aus Gleichung III ebenfalls die Unbekannte 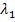 zu eliminieren, addieren wir I und III. Das ergibt die Gleichung III´. In einem weiteren Schritt müssen wir aus III´die nächste Unbekannte
zu eliminieren, addieren wir I und III. Das ergibt die Gleichung III´. In einem weiteren Schritt müssen wir aus III´die nächste Unbekannte 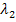 eliminieren. Dadurch kann
eliminieren. Dadurch kann 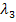 letztendlich leicht berechnet und in II´eingesetzt werden, so dass wir
letztendlich leicht berechnet und in II´eingesetzt werden, so dass wir 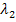 erhalten. Durch Einsetzen von
erhalten. Durch Einsetzen von 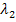 und
und 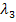 in Gleichung I bekommen wir dann auch
in Gleichung I bekommen wir dann auch 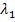 .) Falls dir das beschriebene Vorgehen nicht hundertprozentig klar ist, wiederhole unbedingt das Additionsverfahren im Kapitel Gleichungssysteme:Drei Gleichungen mit drei Unbekannten! Sonst wirst du Schwierigkeiten haben, die nächsten Schritte zu verstehen, obwohl sie oben schon kurz erläutert wurden.
.) Falls dir das beschriebene Vorgehen nicht hundertprozentig klar ist, wiederhole unbedingt das Additionsverfahren im Kapitel Gleichungssysteme:Drei Gleichungen mit drei Unbekannten! Sonst wirst du Schwierigkeiten haben, die nächsten Schritte zu verstehen, obwohl sie oben schon kurz erläutert wurden.
Hier noch einmal das Gleichungssystem:
I 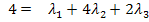
II 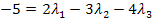
III 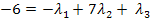
I 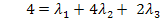
2I – II 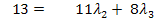 (Gleichung II´)
(Gleichung II´)
I + III 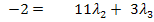 (Gleichung III´)
(Gleichung III´)
I![]()
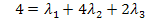
II´![]()
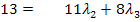
II´- III´  (Gleichung III´´)
(Gleichung III´´)
III´´![]()
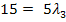 |
| 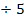
![]()
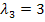
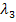 in II´
in II´ 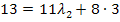
![]()
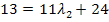
![]() |
| 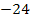
![]()
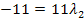
![]() |
| 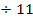
![]()
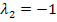
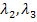 in I
in I 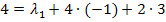
![]()
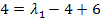
![]()
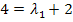
![]() |
| 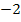
![]()
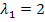
Nun haben wir alle drei Unbekannten ermittelt. 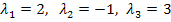
Das Gleichungssystem war eindeutig lösbar, d.h. es ergab sich für jede Unbekannte genau eine Lösung. Es gibt hier also genau eine Linearkombination. Um sie zu erhalten, muss man nur noch die berechneten Werte für 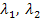 und
und 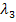 in den allgemeinen Ansatz der Linearkombination
in den allgemeinen Ansatz der Linearkombination 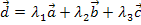 einsetzen. Das ergibt:
einsetzen. Das ergibt:
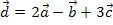
Damit ist die Aufgabe gelöst. Es bleibt noch anzumerken, dass sich bei anderen Aufgaben dieser Art manchmal unendlich viele oder auch gar keine Lösungen für 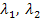 und
und 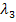 aus dem Gleichungssystem ergeben. Es kann sich bei der Gleichung III´´nämlich auch um eine wahre Aussage, z. B. 4 = 4 oder 0 = 0, handeln oder um einen Widerspruch, z. B. 4 = 3 oder 1 = 0.
aus dem Gleichungssystem ergeben. Es kann sich bei der Gleichung III´´nämlich auch um eine wahre Aussage, z. B. 4 = 4 oder 0 = 0, handeln oder um einen Widerspruch, z. B. 4 = 3 oder 1 = 0.
Ergibt sich eine wahre Aussage, hat das Gleichungssystem unendlich viele Lösungen. Es gibt dann unendlich viele verschiedene Möglichkeiten den Vektor 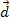 als Linearkombination der drei Vektoren
als Linearkombination der drei Vektoren 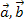 und
und  darzustellen, weil sich alle vier Vektoren in einer gemeinsamen Ebene befinden. Die drei Vektoren
darzustellen, weil sich alle vier Vektoren in einer gemeinsamen Ebene befinden. Die drei Vektoren 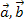 und
und  sind somit linearabhängig/komplanar und liegen daher in einer Ebene, in der sich auch der vierte Vektor
sind somit linearabhängig/komplanar und liegen daher in einer Ebene, in der sich auch der vierte Vektor 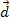 befindet.
befindet.
Ergibt sich ein Widerspruch, hat das Gleichungssystem keine Lösung. Es gibt dann keine Möglichkeit den Vektor 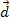 als Linearkombination der drei Vektoren
als Linearkombination der drei Vektoren 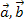 und
und  darzustellen, weil sich die drei Vektoren
darzustellen, weil sich die drei Vektoren 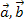 und
und  in einer gemeinsamen Ebene befinden, aber der vierte Vektor
in einer gemeinsamen Ebene befinden, aber der vierte Vektor 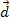 nicht in dieser Ebene liegt. Die Vektoren
nicht in dieser Ebene liegt. Die Vektoren 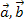 und
und  sind also wieder linear abhängig/komplanar, aber
sind also wieder linear abhängig/komplanar, aber 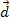 liegt nicht mit ihnen in einer Ebene.
liegt nicht mit ihnen in einer Ebene.
Zusammenfassung:
Es gibt drei verschiedene Möglichkeiten beim Versuch einen Vektor 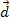 als Linearkombination dreier Vektoren
als Linearkombination dreier Vektoren 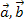 und
und  darzustellen.
darzustellen.
· Die Vektoren 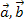 und
und  sind linear unabhängig/nicht komplanar, d.h. sie spannen einen Raum auf. In diesem Raum liegt natürlich auch
sind linear unabhängig/nicht komplanar, d.h. sie spannen einen Raum auf. In diesem Raum liegt natürlich auch 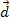 . Daher kann
. Daher kann 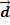 eindeutig als Linearkombination der Vektoren
eindeutig als Linearkombination der Vektoren 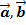 und
und 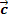 ausgedrückt werden. Das Gleichungssystem liefert wie im 2. Bsp. jeweils genau eine Lösung für die Unbekannten
ausgedrückt werden. Das Gleichungssystem liefert wie im 2. Bsp. jeweils genau eine Lösung für die Unbekannten 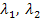 und
und 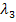 .
.
· Die Vektoren 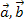 und
und  sind linear abhängig/ komplanar, d.h. sie liegen in einer gemeinsamen Ebene, in der sich zusätzlich auch der Vektor
sind linear abhängig/ komplanar, d.h. sie liegen in einer gemeinsamen Ebene, in der sich zusätzlich auch der Vektor 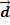 befindet. Es existieren dann unendlich viele verschiedene Möglichkeiten für Linearkombinationen des Vektors
befindet. Es existieren dann unendlich viele verschiedene Möglichkeiten für Linearkombinationen des Vektors 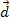 aus den drei Vektoren
aus den drei Vektoren 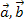 und
und  . Das Gleichungssystem liefert unendlich viele Lösungen für die Unbekannten
. Das Gleichungssystem liefert unendlich viele Lösungen für die Unbekannten 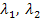 und
und 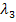 . Es entsteht beim Gauß-Verfahren mindestens eine wahre Aussage.
. Es entsteht beim Gauß-Verfahren mindestens eine wahre Aussage.
· Die Vektoren 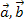 und
und  sind linear abhängig/ komplanar, d.h. sie liegen in einer gemeinsamen Ebene, aber der Vektor
sind linear abhängig/ komplanar, d.h. sie liegen in einer gemeinsamen Ebene, aber der Vektor 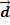 befindet sich nicht in dieser Ebene. Es gibt dann keine Linearkombination des Vektors
befindet sich nicht in dieser Ebene. Es gibt dann keine Linearkombination des Vektors 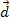 aus den drei Vektoren
aus den drei Vektoren 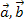 und
und  . Das Gleichungssystem liefert gar keine Lösung für die Unbekannten
. Das Gleichungssystem liefert gar keine Lösung für die Unbekannten 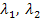 und
und 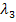 . Es entsteht beim Gauß-Verfahren mindestens ein Widerspruch.
. Es entsteht beim Gauß-Verfahren mindestens ein Widerspruch.
Bitte überlege dir jetzt noch einmal, welche Bedingung für die Vektoren 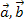 und
und  gelten muss, damit jeder beliebige vierte Vektor
gelten muss, damit jeder beliebige vierte Vektor 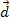 eindeutig als Linearkombination aus ihnen dargestellt werden kann, dass es also wirklich genau eine Linearkombination gibt und nicht unendlich viele oder gar keine!
eindeutig als Linearkombination aus ihnen dargestellt werden kann, dass es also wirklich genau eine Linearkombination gibt und nicht unendlich viele oder gar keine!
Du hast sicher herausgefunden, dass die Vektoren 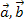 und
und  linear unabhängig sein müssen, damit sich jeder beliebige Vektor
linear unabhängig sein müssen, damit sich jeder beliebige Vektor 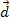 eindeutig als Linearkombination aus ihnen darstellen lässt. Drei Vektoren im
eindeutig als Linearkombination aus ihnen darstellen lässt. Drei Vektoren im 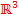 , durch die jeder beliebige Vektor als Linearkombination dargestellt werden kann, nennt man eine „Basis“. Drei Vektoren bilden nur dann eine Basis im
, durch die jeder beliebige Vektor als Linearkombination dargestellt werden kann, nennt man eine „Basis“. Drei Vektoren bilden nur dann eine Basis im 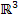 , wenn sie linear unabhängig sind. Entsprechend braucht man im
, wenn sie linear unabhängig sind. Entsprechend braucht man im 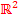 zwei linear unabhängige Vektoren für eine Basis. Mehr dazu unter dem Stichwort Basis.
zwei linear unabhängige Vektoren für eine Basis. Mehr dazu unter dem Stichwort Basis.

