Lineare Ungleichungen
Lineare Ungleichungen sind einfache Ungleichungen ohne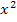 
und ohne x im Nenner. Eine Ungleichung enthält immer ein Ungleichheitszeichen zwischen linker und rechter Seite, also eines der folgenden Zeichen:
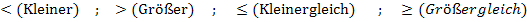
Die Ungleichung – 4x + 3 >1 – 2x wäre zum Beispiel eine lineare Ungleichung. Sie lässt sich durch Umstellen nach x im Prinzip wie eine Gleichung durch Äquivalenzumformungen lösen. Bei einer Ungleichung ist jedoch zu beachten, dass sich bei der Division durch eine negative Zahl bzw. der Multiplikation mit einer negativen Zahl das Ungleichheitszeichen umdreht. (Diese Regel heißt „Inversionsgesetz“.)
Beispiel für die Anwendung des Inversionsgesetzes:
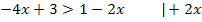
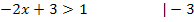
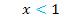
Weil im letzten Schritt durch eine negative Zahl geteilt wird, muss das Ungleichheitszeichen umgedreht werden;das besagt das Inversionsgesetz.
Die Lösungsmenge einer linearen Ungleichung hängt von der jeweils geltenden Grundmenge ab. (Die Grundmenge G ist die Menge aller Zahlen, aus der die Zahlen x stammen.) Wenn nichts anderes angegeben ist, gilt bis zur 8. Klasse G = ℚ und ab der 9. Klasse G = ℝ
In manchen Aufgaben ist aber auch eine andere Grundmenge angegeben, wie zum Beispiel Grundmenge G = ℕ. In diesem Fall kann x nur eine natürliche Zahl, also eine positive ganze Zahl ausschließlich Null sein.
Die oben gezeigte Ungleichung hätte in der Grundmenge G = ℕkeine Lösung, denn es gibt keine natürliche Zahl, die die Ungleichung x <1 erfüllt. Die Lösungsmenge L wäre dann die leere Menge:L =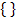 
In der Grundmenge G = ℚ oder in G = ℝwürde die Lösungsmenge der oben gezeigten Ungleichung dagegen lauten: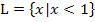 
oder in der Intervallschreibweise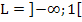 
Manche lineare Ungleichungen sind auch allgemein gültig;d.h. die Aussage ist für jedes x aus der Grundmenge G grundsätzlich wahr. Dann ist die Lösungsmenge gleich der Grundmenge.
Beispiel einer allgemeingültigen linearen Ungleichung:
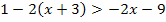
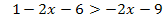
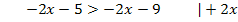
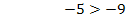
Man erkennt sofort, dass die Aussage immer wahr ist – egal was für x eingesetzt wird, denn am Ende kommt ja gar kein x mehr vor.
