Laplace-Wahrscheinlichkeit

Die Laplace-Wahrscheinlichkeit eines Ereignisses E berechnet man mit der Formel:

P(E) = 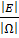In Worten:P(E) =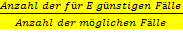

Wichtig:Absolute Voraussetzung für diese Formel ist die Gleichwahrscheinlichkeit aller Fälle! Alle einzelnen Fälle müssen mit der gleichen Wahrscheinlichkeit kommen, andernfalls gilt die oben gezeigte Formel für die Wahrscheinlichkeit nicht!

Anmerkung:Mit den „günstigen“ Fällen sind die Fälle gemeint, die zu dem Ereignis gehören, nach dessen Wahrscheinlichkeit gefragt ist.

Beispiel:

Wie großist die Wahrscheinlichkeit, dass beim Wurf eines L-Würfels, d.h. eines Würfels, bei dem jede Seite mit der gleichen Wahrscheinlichkeit kommt, die Augenzahl Sechs geworfen wird?

Lösung:

Es handelt sich um einen Laplace-Würfel, kurz L-Würfel, also um einen nicht gezinkten Würfel. Daher erscheint jede Seite mit der gleichen Wahrscheinlichkeit. Der Würfel kann die Augenzahlen von 1 bis 6 zeigen.

Anzahl der möglichen (gleichwahrscheinlichen) Fälle: 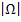= 6

Das Ereignis E, nach dessen Wahrscheinlichkeit gefragt ist, lautet „Augenzahl Sechs“.

E =:„Augenzahl Sechs“

Nur auf einer Seite steht die Augenzahl 6, also gibt es nur einen für E günstigen Fall: 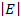= 1

Die Wahrscheinlichkeit für das Ereignis E berechnet sich dann folgendermaßen:

P(E) = 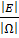= 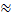0,1667 = 16,67%

Vorsicht:Umgangssprachlich sagt man zwar oft, die Wahrscheinlichkeit für „Sechs“ ist Eins zu Fünf, das darf aber keinesfalls mit 1 :5 geschrieben werden. Die Wahrscheinlichkeit ist schließlich nicht 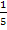, sondern ! Das wird sofort klar, wenn man sich überlegt, mit welcher Wahrscheinlichkeit beim Wurf einer L-Münze das Ereignis „Zahl“ kommt. Dir ist sicher klar, dass die Zahl mit 50% Wahrscheinlichkeit kommt. Die Münze hat zwei (gleichwahrscheinliche) Seiten;nur auf einer Seite steht die Zahl. Es gibt also zwei mögliche und einen günstigen Fall. Die Wahrscheinlichkeit ist daher 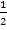= 0,5 = 50% und nicht etwa        1 :1= 1 = 100%.

Weitere Beispiele findest du im Bereich Stochastik im Kapitel Laplace-Wahrscheinlichkeit. Wie man die Anzahl der möglichen Fälle, d.h. die Mächtigkeit des Ergebnisraums 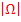, und die Anzahl der günstigen Fälle bei umfangreicheren Aufgaben berechnen kann, wird im Kapitel Kombinatorik erklärt.