Kürzen
Kürzen bedeutet, im Zähler und Nenner eines Bruchs zugleich durch die gleiche Zahl zu dividieren.
Beispiel:
Kürzen mit der Zahl 2: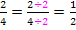 
Durch das Kürzen ändert sich der Wert des Bruchs nicht. Stell dir dazu einfach einen runden Kuchen vor:Zwei Viertel ist genauso viel wie ein halber Kuchen.
Durch geschicktes Kürzen kann ein Bruch oder Bruchterm (d.h. ein Bruch, der eine Variable z.B. x enthält) aber eventuell vereinfacht werden. Wenn du merkst, dass sich ein Bruch kürzen lässt, solltest du es auch auf jeden Fall gleich machen. Es ist zwar nicht wirklich falsch mit ungekürzten Brüchen zu rechnen, aber es ist wesentlich umständlicher. Endergebnisse müssen allerdings immer in vollständig gekürzter Form angegeben werden.
Kürzen darf man allerdings nur, wenn im Zähler und im Nenner des Bruchs keine Summe oder Differenz vorliegt.
Ein blöder, aber hilfreicher Merkspruch:
„Aus Differenzen und Summen kürzen nur die Dummen!“
Soll nicht heißen, dass du dumm bist, bloßweil du schon einmal den Fehler gemacht hast aus einer Summe oder Differenz zu kürzen. Dieser Fehler ist schon vielen Schülern vor dir passiert und wird auch sicher noch vielen passieren! Doch kürzen kannst du eben nur dann, wenn ein Produkt, also eben keine Summe oder Differenz, im Zähler und Nenner des Bruchs vorliegt.
Beispiele für Brüche / Bruchterme, die sich kürzen lassen:
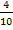Kürzen mit der Zahl 2 
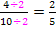
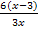Kürzen mit der Zahl 3 
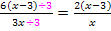
Vorsicht:Das x oder die Zahl 3 in der Klammer dürfen nicht einzeln gekürzt werden, denn der Ausdruck x – 3 ist eine Differenz, und aus Differenzen und Summen kürzen nur die …
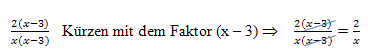
Die ganze Klammer (x – 3) darf insgesamt gekürzt werden, aber eben nicht x oder 3 einzeln!
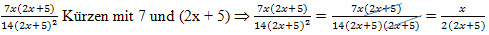
Beispiele für Brüche, die sich erst nach geeigneter Umformung (z.B. durch Ausklammern oder binomische Formeln) kürzen lassen:
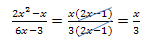
Dieses Beispiel ist nur für Schüler, welche die Binomischen Formeln bereits gelernt haben, geeignet:
Der nächste Bruch lässt sich mit Hilfe eines keinen Tricks so umformen, dass man kürzen kann. Der Trick besteht darin, ein Minuszeichen (genau genommen die Zahl -1) auszuklammern.
Merke:Durch das Ausklammern eines Minuszeichens dreht sich die Reihenfolge bei einer Differenz um! Es gilt:
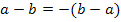
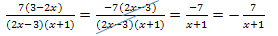Anmerkung:Man hätte das Minuszeichen genauso gut im Nenner ausklammern können. Das führt letztendlich zum gleichen Endergebnis:
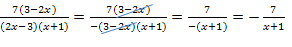In vielen verschiedenen Aufgaben muss gekürzt werden, um die auftretenden Brüche oder Bruchterme zu vereinfachen. Daher ist es absolut unerlässlich, dass du sofort erkennst, wann man kürzen kann. Mehr Aufgabenbeispiele zum Thema Kürzen von Bruchtermen findest du im Bereich Algebra im Kapitel Bruchterme.
