Konstruktion
Unter einer Konstruktion versteht man eine Zeichnung, die nur mit Lineal und Zirkel angefertigt wird. Es darf natürlich an Stelle des Lineals auch ein Geodreieck benützt werden, jedoch ohne dabei irgendwelche Winkel abzumessen. Streng genommen dürfen bei einer Konstruktion auch keine Längen abgemessen werden. Eigentlich müsste man also vorher die entsprechende Länge an einer gesonderten Stelle auf dem Blatt zeichnen; dabei muss man die Länge der Strecke natürlich noch mit dem Lineal bzw. Geodreieck abmessen. Danach wird die Strecke mit dem Zirkel abgegriffen und an die richtige Stelle in der Konstruktion übertragen. Bei der Aufgabenstellung „ Konstruiere …!“ dürfen also weder Längen noch Winkel mit dem Winkelmesser, Geodreieck oder Lineal abgemessen werden. Etwas anderes ist es, wenn in der Aufgabe verlangt ist, dass irgendeine Figur gezeichnet werden soll. Bei einer Zeichnung ist es erlaubt, Längen und Winkel einfach abzumessen. Unterscheide daher genau zwischen einfacher Zeichnung und echter Konstruktion! Konstruktionen werden hauptsächlich im Gymnasium, selten in der Realschule verlangt. Die meisten Lehrer, auch im Gymnasium, sehen heute den Begriff der Konstruktion etwas lockerer: Längen müssen daher bei den meisten Lehrern auch in Konstruktionen nicht mehr vorher in eine gesonderte Ecke des Blattes gezeichnet und dann übertragen werden. Längen können also auch bei Konstruktionen direkt mit dem Lineal bzw. Geodreieck abgemessen werden. Winkel müssen aber wirklich konstruiert, also nur mit Zirkel und Lineal gezeichnet werden. Besonders rechte Winkel, 30°-, 45°- oder 60°- Winkel müssen besonders oft konstruiert werden. Dazu verwendest du bestimmte Grundkonstruktionen, wie z.B. Lot errichten, Lotfällen, Winkelhalbierende konstruieren usw. Ein 60°-Winkel lässt sich beispielsweise ganz leicht mit Hilfe eines gleichseitigen Dreiecks konstruieren. Da ein Gleichseitiges Dreieck drei gleich lange Seiten hat, hat es drei gleich große Winkel. Alle drei Innenwinkel eines Dreiecks ergeben zusammen bekanntlich 180°, daher hat einer der drei Winkel 180° : 3 = 60°. Um einen 60°-Winkel zu konstruieren, braucht man also nur irgendein gleichseitiges Dreieck konstruieren; jeder Innenwinkel beträgt dann 60°.
Beispiel: Konstruktion eines 60°-Winkels
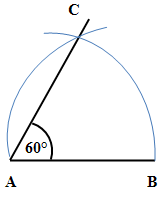
Wie in der Skizze gezeigt, legt man eine Strecke [AB] beliebig fest. Dann zeichnet man jeweils einen Kreis um die Punkte A und B mit Radius r = . Man greift also die Strecke mit dem Zirkel ab und zeichnet mit diesem Radius die beiden Kreise um A und B. Diese Kreise schneiden sich im Punkt C. Nun zeichnet man beispielsweise die Halbgerade von A durch C. Der entstehende Winkel beträgt 60°.

