Kombinatorik
Die Kombinatorik ist ein Teilgebiet der Wahrscheinlichkeitsrechnung/Stochastik. Die Kombinatorik ist die Berechnung der Anzahl aller möglichen Fälle eines Zufallsexperiments oder eines bestimmten Ereignisses. Mit Hilfe der sogenannten kombinatorischen Hilfsmittel, wie zum Beispiel des Binomialkoeffizienten oder der Fakultät, kann berechnet werden, wie viele verschiedene Ergebnisse bei einem Zufallsexperiment herauskommen können, also die Mächtigkeit des Ergebnisraums. Man muss also nicht erst alle Möglichkeiten aufschreiben und dann abzählen, wie viele es sind, sondern kann mit Hilfe der Kombinatorik direkt ausrechnen, wie viele verschiedene Möglichkeiten existieren. Dies ist bei der Berechnung von Laplace-Wahrscheinlichkeiten sehr hilfreich, vor allem dann, wenn es sehr viele verschiedene Möglichkeiten gibt.
Beispiel einer typischen (leichten) Kombinatorik-Aufgabe:
In einer Tiefgarage gibt es 20 Stellplätze. Wie viele verschiedene Möglichkeiten gibt es, drei unterscheidbare Autos in dieser Tiefgarage zu parken?
Lösung:
Wir überlegen uns Folgendes:Die drei Autos sind laut Angabe unterscheidbar, beispielsweise ein blaues, ein grünes und ein rotes Auto. Gehen wir ´mal davon aus, dass wir zuerst das blaue, dann das grüne und zuletzt das rote Auto parken. Für das blaue Auto, das wir als erstes in der Tiefgarage parken, stehen noch alle 20 Stellplätze zur Verfügung. Es gibt also 20 Möglichkeiten für das blaue Auto. Nun wird als nächstes das grüne Auto in der Tiefgarage geparkt. Dafür stehen nur noch 19 Stellplätze zu Verfügung, denn auf einem Platz steht schon das vorher geparkte blaue Auto. Somit gibt es 19 Möglichkeiten für das grüne Auto. Als drittes und letztes kommt jetzt das rote Auto. Für dieses Auto gibt es nur 18 Möglichkeiten der Platzierung, denn von den 20 Stellplätzen in der Tiefgarage sind schließlich schon zwei durch die vorher geparkten anderen beiden Autos besetzt. Die 20 Möglichkeiten für das erste Auto müssen nun alle mit den 19 Möglichkeiten für das zweite und mit den 18 Möglichkeiten für das dritte kombiniert, d.h. multipliziert werden. Daher existieren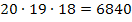 
Möglichkeiten drei unterscheidbare Autos auf 20 Plätze zu verteilen.
Die gezeigte Beispielaufgabe war noch nicht schwer. Leider können Kombinatorik-Aufgaben ganz schön verzwickt sein, da man zwar gewisse Grundprinzipien relativ schnell lernt, sie jedoch oft miteinander kombinieren können muss, um selbst auf die Lösung zu kommen. Typischerweise leuchtet einem die Lösung sehr wohl ein, wenn man sie einmal zu sehen bekommen hat, jedoch ist es für die meisten Schüler schwer selbst auf die Lösung einer neuen Aufgabe zu kommen. Das erfordert viel Übung! Erfreulicherweise wird aber in Bayern aktuell sowohl im Fachabitur als auch im G8-Abitur kein so großer Wert mehr auf Kombinatorik gelegt. (Im G9-Abitur kamen deutlich mehr und wesentlich schwierigere Kombinatorik-Aufgaben vor.) Ausführlichere Erklärungen findest du im Kapitel Kombinatorische Hilfsmittel:Zählprinzip, Fakultät und Binomialkoeffizient.
