Intervallschreibweise
An Stelle von Ungleichungen wird häufig die Intervallschreibweise verwendet, da sie sehr übersichtlich und kurz ist. Um einen durchgehenden Zahlenbereich, also ein Intervall zu beschreiben, werden immer eckige Klammern verwendet, keine geschweiften Klammern.
Vorsicht Verwechslungsgefahr:
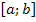beschreibt den ganzen Zahlenbereich von a bis b (beide Grenzen eingeschlossen)
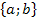beschreibt die Menge, die nur die zwei Zahlen a und b enthält, nicht aber die Zahlen dazwischen. Es handelt sich also nur um eine Aufzählung von Zahlen, aber nicht um ein Intervall!
Merke: Verwende eckige Klammern für einen durchgehenden Zahlenbereich, also für ein Intervall! Nimm geschweifte Klammern für die Aufzählung einzelner Zahlen!
Besondere Aufmerksamkeit muss auch den Grenzen des Zahlenbereichs gewidmet werden. Soll die jeweilige Grenze ausgeschlossen werden, so ist die eckige Klammer nach außen gerichtet, zeigt also von der Zahl weg. Soll allerdings die jeweilige Grenze miteingeschlossen werden, dann zeigt die eckige Klammer nach innen, also zu der Zahl hin. Es kann auch eine Grenze ein- und die Andere ausgeschlossen sein, wie du an den gleich folgenden Beispielen b) und c) erkennen kannst.
Beispiele: Alle folgenden Beispiele beziehen sich auf die größtmögliche Grundmenge, die du bereits kennst. G=ℚ (oder, wenn du schon Wurzeln gelernt hast, G=ℝ) Einfacher gesagt: x kann eine beliebige Zahl sein, z.B. eine ganze Zahl, eine Dezimalzahl (Kommazahl) oder ein Bruch.
a)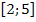 
beschreibt die Menge aller Zahlen von einschließlich 2 bis ebenfalls einschließlich 5. In anderen Worten:Die Zahlen von mindestens 2 bis höchstens 5
D.h. beide Ränder sind jeweils eingeschlossen.
b)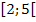 
beschreibt die Menge aller Zahlen von einschließlich 2 bis ausgeschlossen 5. Einfacher gesagt:Die Zahl 2 ist noch in der Menge enthalten, die Zahl 5 jedoch nicht. Zahlen wie z.B. 4,9999 oder 4,9999999 liegen aber noch innerhalb dieser Menge.
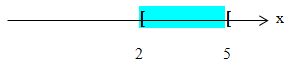
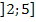beschreibt die Menge aller Zahlen von ausgeschlossen 2 aber eingeschlossen 5. Das bedeutet, dass die Zahl 2 nicht mehr in dieser Menge liegt, die Zahl 5 aber schon noch. Zahlen wie z.B. 2,000001 oder 2,0001 liegen dagegen auch noch darin.
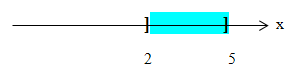
d)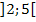 
beschreibt die Menge aller Zahlen von ausgeschlossen 2 bis ebenfalls ausgeschlossen 5, da beide Klammern nach außen, also von den Zahlen 2 und 5 weg gerichtet sind. Diese Menge enthält also nur Zahlen, die größer als 2 aber auch gleichzeitig kleiner als 5 sind. Zahlen wie z.B. 2,000001 oder 4,99999 liegen aber noch innerhalb.
e)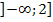 
beschreibt die Menge aller Zahlen, die kleiner oder gleich 2 sind. D.h. die Grenze 2 ist noch eingeschlossen, da die eckige Klammer nach innen zur Zahl 2 hin gerichtet ist. Die Klammer bei 
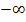(Sprich:„Minus-Unendlich“) zeigt nach außen;da Minus-Unendlich keine normale Zahl ist, wird es immer ausgeschlossen.
f)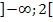 
beschreibt die Menge aller Zahlen, die kleiner als 2 sind. Die Grenze 2 ist hier ausgeschlossen, da die eckige Klammer von der Zahl 2 weg gerichtet ist. Zahlen wie z.B. 1,99999 oder 1,99999999 liegen aber noch innerhalb dieser Menge.
g)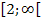 
beschreibt die Menge aller Zahlen, die größer oder gleich 2 sind. Die Grenze 2 ist noch eingeschlossen, da die eckige Klammer nach innen, also zur 2 hin gerichtet ist. Die Klammer bei 
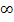(Sprich:„Unendlich“) zeigt nach außen;da Unendlich – genauso wie Minus-Unendlich – keine echte Zahl ist, wird es immer ausgeschlossen.
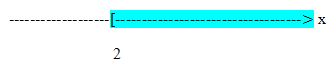
h)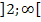 
beschreibt die Menge aller Zahlen, die größer als 2 sind. Die Grenze 2 ist hier ausgeschlossen, da die eckige Klammer von der Zahl 2 weg gerichtet ist. Zahlen wie z.B. 2,0000001 oder 2,00001 liegen aber noch innerhalb dieser Menge. Unendlich ist natürlich, wie vorher bereits erläutert, ausgeschlossen.
