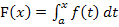Integralfunktion
Eine Funktion, die sich in der Form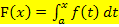 
schreiben lässt, heißt Integralfunktion. Die untere Grenze des Integrals a ist eine beliebige reelle Zahl, also eine feste Zahl. Die obere Grenze ist die Variable x und somit natürlich variabel. Die Funktion 
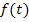ist die Integrandenfunktion, kurz Integrand;d.h. 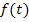ist die Funktion, die integriert werden muss. (Zur Erinnerung:Das Integrieren ist das Gegenteil des Ableitens. Siehe auch:Ableitung)
Beispiel: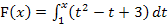 
Im Unterschied zur Integralfunktion, die immer die variable obere Grenze x hat, hat das bestimmte Integral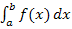 
zwei feste Grenzen a und b. Das bestimmte Integral entspricht der Fläche zwischen 
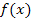, den senkrechten Geraden x = a und x = b sowie der x-Achse, zumindest dann wenn der Graph von 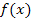oberhalb der x-Achse verläuft. Liegt die Fläche unterhalb der x-Achse ist das bestimmte Integral negativ. Das Integral 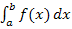ist die sogenannte Flächenbilanz, d.h. Flächenanteile oberhalb der x-Achse werden positiv gezählt, die unterhalb der x-Achse negativ.)
Das unbestimmte Integral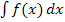 
hat dagegen überhaupt keine Grenzen.
Unbestimmtes Integral (Menge aller Stammfunktionen):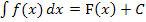 
Bestimmtes Integral (Flächenbilanz): Integralfunktion (Flächenbilanzfunktion): |
Für jede Integralfunktion gilt: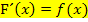 
Um die Ableitung einer Integralfunktion zu finden, muss also bloßdie Funktion hinter dem Integralzeichen genommen werden und jedes auftretende x durch t ersetzt werden. Man muss also nicht zuerst integrieren und dann wieder ableiten, wenn man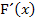 
sucht. Die untere Grenze spielt dabei keine Rolle.
Beispiel: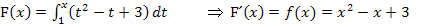 
Laut Definition ist jede Funktion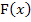 
eine Stammfunktion zu 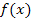, für die 
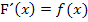erfüllt ist. Da bei jeder Integralfunktion der Zusammenhang 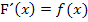gilt, ist jede Integralfunktion auch Stammfunktion zu 
.
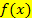Umgekehrt ist aber nicht jede Stammfunktion auch Integralfunktion. Das liegt daran, dass jede Integralfunktion bei x = a, also bei der unteren Grenze eine Nullstelle besitzt und somit mindestens eine Nullstelle hat. Ein Integral von a bis a ist zwangsläufig gleich Null, weil keine Fläche zwischen x = a und x = a liegt: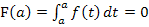 
Jede Integralfunktion besitzt also mindestens eine Nullstelle, eine Stammfunktion muss dagegen keine Nullstelle haben. Daher sind nur diejenigen Stammfunktionen, die mindestens eine Nullstelle besitzen, auch Integralfunktionen. Stammfunktionen ohne Nullstelle sind keine Integralfunktionen.
Mehr dazu im Kapitel Einführung in die Integralrechnung im Teil Die Integralfunktion und der HDI.
