Integral/Integrieren

Das Integrieren ist praktisch das Gegenteil des Ableitens. (Siehe auch:Ableitung) Integriert man eine Funktion 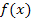, so ergibt sich eine Stammfunktion F(x) zur Funktion 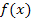. Die Ableitung F´(x) der Stammfunktion F(x) ist wieder die Funktion 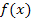. Genau das besagt auch der Hauptsatz der Differenzial- und Integralrechnung (HDI):

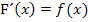
Man unterscheidet zwischen dem bestimmten Integral 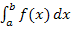und dem unbestimmten Integral .

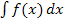Besonders bei der Berechnung von Flächen zwischen dem Graph einer Funktion 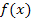und der x-Achse oder einer Fläche zwischen zwei Funktionen braucht man das Integral. Wie man ein Integral berechnet, d.h. wie man integriert, ist kurz erklärt bei Bestimmtes Integral und auch bei Unbestimmtes Integral.

Ausführliche Erklärungen und ganz viele Beispiele gibt´s im Kapitel Einführung in die Integralrechnung.

---