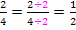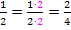Hauptnenner
Als Hauptnenner bezeichnet man den gemeinsamen Nenner zweier oder mehrerer Brüche. Er ist das kleinste gemeinsame Vielfache der Nenner der einzelnen Brüche. Du weißt aus der 6. Klasse bestimmt noch:Man muss Brüche immer erst auf den Hauptnenner bringen, um sie addieren oder subtrahieren zu können, da nur Brüche mit gleichem Nenner direkt addiert oder subtrahiert werden können.
| Zur Erinnerung:
Um jedoch Brüche, die noch nicht den gleichen Nenner besitzen, addieren zu können, müssen sie zuerst auf einen gemeinsamen Nenner, den Hauptnenner, gebracht werden. Das wird durch entsprechendes Erweitern der beiden Brüche gemacht. Erweitern bedeutet, im Zähler und Nenner eines Bruchs zugleich mit der gleichen Zahl zu multiplizieren. Der Wert eines Bruchs ändert sich durch das Erweitern nicht. Das Erweitern ist ja nur das Gegenteil des Kürzens und beim Kürzen ändert sich der Wert eines Bruchs schließlich ebenfalls nicht. Kürzen bedeutet, im Zähler und Nenner eines Bruchs zugleich durch die gleiche Zahl zu dividieren. Das kannst du dir auch leicht an einem in Stücke geschnittenen Kuchen vorstellen. Ob du nun zwei Viertel-Stücke oder einen halben Kuchen hast, das ist ja mengenmäßig das Gleiche. Daher gilt: Von Kürzen mit der Zahl 2: |
Sollen z.B. die beiden Brüche  und
und 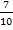 addiert werden, müssen sie erst auf einen gemeinsamen Nenner gebracht werden. Wir brauchen also einen Nenner, auf den sich beide Brüche erweitern lassen. Außerdem soll der gemeinsame Nenner möglichst klein sein, weil es sich mit kleinen Zahlen einfach besser rechnet. Der Hauptnenner von
addiert werden, müssen sie erst auf einen gemeinsamen Nenner gebracht werden. Wir brauchen also einen Nenner, auf den sich beide Brüche erweitern lassen. Außerdem soll der gemeinsame Nenner möglichst klein sein, weil es sich mit kleinen Zahlen einfach besser rechnet. Der Hauptnenner von  und
und 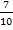 ist daher das kleinste gemeinsame Vielfache von 6 und 10, nämlich die Zahl 30. Sowohl der Bruch
ist daher das kleinste gemeinsame Vielfache von 6 und 10, nämlich die Zahl 30. Sowohl der Bruch  als auch der Bruch
als auch der Bruch 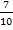 lässt sich auf den Nenner 30 bringen. Der Bruch
lässt sich auf den Nenner 30 bringen. Der Bruch  muss mit der Zahl 5 erweitert werden, um auf den Nenner 30 gebracht zu werden. Den Bruch
muss mit der Zahl 5 erweitert werden, um auf den Nenner 30 gebracht zu werden. Den Bruch 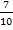 muss man mit 3 erweitern, um ihn auf den Nenner 30 zu bringen. Es gibt keine kleinere Zahl, auf die sich beide Nenner erweitern lassen, als die Zahl 30. Daher ist 30 hier das kleinste gemeinsame Vielfache von 6 und 10, also der Hauptnenner.
muss man mit 3 erweitern, um ihn auf den Nenner 30 zu bringen. Es gibt keine kleinere Zahl, auf die sich beide Nenner erweitern lassen, als die Zahl 30. Daher ist 30 hier das kleinste gemeinsame Vielfache von 6 und 10, also der Hauptnenner.
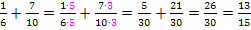
Viele Schüler haben ihre liebe Not, den Hauptnenner bei etwas anspruchsvolleren Aufgaben zu finden. Oft ist der Hauptnenner einfach das Produkt der einzelnen Nenner. Leider stimmt das nicht immer, was du schon am oben gezeigten Beispiel sehen kannst. Wenn man die Nenner der beiden Brüche  und
und 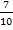 einfach nur multipliziert, erhält man ja
einfach nur multipliziert, erhält man ja 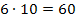 und nicht den Hauptnenner 30! 60 ist nämlich nicht das kleinste gemeinsame Vielfache von 6 und 10, sondern nur irgendein Vielfaches. Wie findest du nun aber auch bei schwierigeren Fällen den Hauptnenner? Da hilft eigentlich nur eine sogenannte Primfaktorzerlegungbei Zahlen bzw. eine vollständige Faktorisierung von Ausdrücken, die x enthalten. (Faktorisieren bedeutet das Selbe, wie in ein Produkt umformen.) Man zerlegt jede Zahl, die im Nenner vorkommt, vollständig in Primfaktoren und faktorisiert die Faktoren, die x enthalten, so weit möglich z.B. durch ausklammern. Dann schaust du, bei welchem Nenner jeder Primfaktor jeweils am häufigsten, also mit der höchsten Potenz, vorkommt. So oft kommt dieser Primfaktor dann im Hauptnenner vor. So gehst du bei jedem auftretenden Primfaktor und entsprechend bei den Faktoren vor, die x enthalten. Falls dir das noch nicht wirklich klar geworden ist, ist das nicht schlimm. Am besten schauen wir uns einfach ein konkretes Beispiel an.
und nicht den Hauptnenner 30! 60 ist nämlich nicht das kleinste gemeinsame Vielfache von 6 und 10, sondern nur irgendein Vielfaches. Wie findest du nun aber auch bei schwierigeren Fällen den Hauptnenner? Da hilft eigentlich nur eine sogenannte Primfaktorzerlegungbei Zahlen bzw. eine vollständige Faktorisierung von Ausdrücken, die x enthalten. (Faktorisieren bedeutet das Selbe, wie in ein Produkt umformen.) Man zerlegt jede Zahl, die im Nenner vorkommt, vollständig in Primfaktoren und faktorisiert die Faktoren, die x enthalten, so weit möglich z.B. durch ausklammern. Dann schaust du, bei welchem Nenner jeder Primfaktor jeweils am häufigsten, also mit der höchsten Potenz, vorkommt. So oft kommt dieser Primfaktor dann im Hauptnenner vor. So gehst du bei jedem auftretenden Primfaktor und entsprechend bei den Faktoren vor, die x enthalten. Falls dir das noch nicht wirklich klar geworden ist, ist das nicht schlimm. Am besten schauen wir uns einfach ein konkretes Beispiel an.

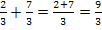
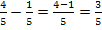
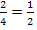
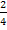 kommt man durch Kürzen mit 2 auf
kommt man durch Kürzen mit 2 auf 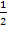 . Umgekehrt kommt man von
. Umgekehrt kommt man von