Gegenereignis
Zu jedem Ereignis E gibt es das sogenannte Gegenereignis 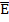 (Sprich:„Nicht-E“). Das Gegenereignis
(Sprich:„Nicht-E“). Das Gegenereignis 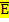 enthält genau die Elementarereignisse des Ergebnisraums
enthält genau die Elementarereignisse des Ergebnisraums 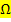 , die nicht zu E gehören. Das Gegenereignis
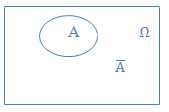
, die nicht zu E gehören. Das Gegenereignis 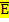 ergibt daher zusammen mit dem Ereignis E wieder den Ergebnisraum
ergibt daher zusammen mit dem Ereignis E wieder den Ergebnisraum  .
.
Für die Wahrscheinlichkeitdes Gegenereignisses gilt:
P( 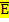 ) = 1- P(E)
) = 1- P(E)![]() bzw. P(
bzw. P(  ) = 100% – P(E)
) = 100% – P(E)
Das ist auch logisch, denn wenn beispielsweise 20% aller Menschen blond (B) sind, dann gibt es natürlich 100% – 20% = 80% nicht-blonde Menschen ( 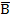 ).
).
Ob man mir Prozent oder mit Dezimalzahlen rechnet, ist an sich egal. Doch empfiehlt sich langfristig eher das Rechnen mit Dezimalzahlen.
P(B) = 20% = 0,2  P(
P( 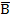 ) = 1- 0,2 = 0,8
) = 1- 0,2 = 0,8
Beispiel:Dreimaliges Werfen einer Münze
Gib den Ergebnisraum 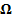 als Menge und die Gegenereignisse zu folgenden Ereignissen in Worten und als Menge (in aufzählender Darstellung) an!
als Menge und die Gegenereignisse zu folgenden Ereignissen in Worten und als Menge (in aufzählender Darstellung) an!
A = „Beim ersten und letzten Wurf Zahl“
B = „Keine Zahl“
C = „Höchstens einmal Wappen“
Lösung:
Der Ergebnisraum 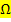 enthält alle möglichen Fälle. Man kann sie entweder mit Hilfe eines Baumdiagrammsoder durch bloße Überlegung ermitteln.
enthält alle möglichen Fälle. Man kann sie entweder mit Hilfe eines Baumdiagrammsoder durch bloße Überlegung ermitteln.
Am einfachsten findet man alle möglichen Ausgänge dieses Zufallsexperiments durch die Überlegung, wie oft beispielsweise das Wappen auftreten kann. Danach überlegt man sich noch bei welchem Versuch das Wappen geworfen wird.
Beachte, dass die Reihenfolge hier wichtig ist! Es macht schließlich einen Unterschied, ob das Wappen beim ersten, zweiten oder beim dritten Wurf kommt!
Im Folgenden sind alle Elemente von 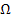 nach der Anzahl der auftretenden Wappen in aufsteigender Reihenfolge genannt:
nach der Anzahl der auftretenden Wappen in aufsteigender Reihenfolge genannt:
Kein Wappen:ZZZ
Genau ein Wappen:WZZ, ZWZ, ZZW
Anmerkung:Das W wurde dabei einfach von vorne nach hinten durchgeschoben;so vergisst man keine Möglichkeit. WZZ bedeutet dabei, dass beim ersten Versuch Wappen, beim zweiten und dritten Wurf Zahl kommt. ZWZ bedeutet entsprechend, dass zuerst Zahl, dann Wappen und dann noch einmal Zahl geworfen wird. ZZW bedeutet also, dass zuerst zweimal Zahl und erst beim dritten Versuch Wappen geworfen wird. Es kommt also bei diesem Beispiel auf die Reihenfolge an.
Genau zweimal Wappen;ZWW, WZW, WWZ
Anmerkung:Damit man keinen möglichen Fall übersieht, schiebt man zum Beispiel das nur einmal auftretende Z von vorne nach hinten durch. ZWW bedeutet natürlich, dass beim ersten Wurf Zahl und beim zweiten und dritten Wurf Wappen kommt. WZW ist dann entsprechend, beim ersten Wurf Wappen, dann Zahl und danach wieder Wappen. WWZ bedeutet dann, beim ersten und zweiten Wurf Wappen, beim dritten Wurf Zahl.
Dreimal Wappen:WWW
Der Ergebnisraum 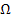 des Zufallsexperiments „dreimaliger Wurf einer Münze“ lautet daher:
des Zufallsexperiments „dreimaliger Wurf einer Münze“ lautet daher:
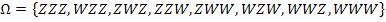
Die Reihenfolge der einzelnen Elemente, den sogenannten Elementarereignissen, spielt dabei keine Rolle. Die hier gezeigte Reihenfolge, nach Anzahl der Wappen geordnet, ist jedoch sehr praktisch:Erstens übersieht man so keine Möglichkeit und zweitens lassen sich dadurch oft die Ereignismengen leichter bilden.
Nun zu den verlangten Gegenereignissen. Ein Gegenereignis enthält immer genau die Fälle des Ergebnisraums 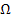 , die nicht zu dem jeweiligen Ereignis selbst gehören. am einfachsten findet man alle Elemente des Gegenereignisses, indem man sich zuerst überlegt, welche Elemente aus
, die nicht zu dem jeweiligen Ereignis selbst gehören. am einfachsten findet man alle Elemente des Gegenereignisses, indem man sich zuerst überlegt, welche Elemente aus 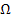 zum Ereignis selbst gehören;die restlichen Elemente aus
zum Ereignis selbst gehören;die restlichen Elemente aus 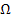 bilden dann das Gegenereignis.
bilden dann das Gegenereignis.
A = „Beim ersten und letzten Wurf (zugleich) Zahl“
A = 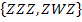
Zur Verdeutlichung markieren wir alle Elemente aus 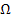 , die zu A gehören farbig. Die Restlichen bilden die Menge des Gegenereignisses
, die zu A gehören farbig. Die Restlichen bilden die Menge des Gegenereignisses 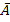 .
.
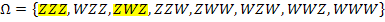
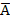 = „Nicht gleichzeitig beim ersten und letzten Wurf Zahl“
= „Nicht gleichzeitig beim ersten und letzten Wurf Zahl“
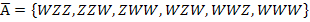
B = „Keine Zahl“
B = 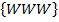
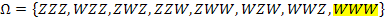
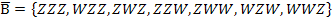
Nun lässt sich das Gegenereignis zu B auch einfacher in Worten formulieren.
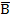 = „Mindestens eine Zahl“ oder „Höchstens zweimal Wappen“
= „Mindestens eine Zahl“ oder „Höchstens zweimal Wappen“
Achtung:Das Ereignis „Nur Zahlen“ bzw. „Dreimal Zahl“ ist nicht das Gegenereignis zu „Keine Zahl“! „Dreimal Zahl“ = 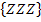 ergänzt sich mit „Keine Zahl“ =
ergänzt sich mit „Keine Zahl“ = 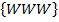 nicht zu
nicht zu 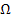 . Daher sind sie keine Gegenereignisse zueinander!
. Daher sind sie keine Gegenereignisse zueinander!
C = „Höchstens einmal Wappen“ d.h. „Keinmal oder genau einmal Wappen, aber nicht öfter“
C = 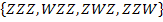
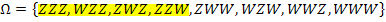
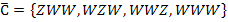
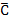 = „Mindestens zweimal Wappen“ oder „Höchstens einmal Zahl“
= „Mindestens zweimal Wappen“ oder „Höchstens einmal Zahl“
Die Aussage „Mindestens zweimal Wappen“ ist natürlich gleichbedeutend mit „Höchstens einmal Zahl“. Wie du es ausdrücken möchtest bleibt dir selbst überlassen. Es ist aber einfacher bei der Beschreibung des Gegenereignisses in Worten bei der Anzahl der Wappen zu bleiben, wenn in der Angabe des Ereignisses bereits die Anzahl der Wappen genannt wurde.
Mehr zu diesem Thema findest du im Bereich Stochastik in den Kapiteln Gegenereignis und Wahrscheinlichkeit.

