Gebrochenrationale Funktionen

Eine gebrochenrationale Funktion ist eine Funktion vom Typ

In einfachen Worten: Es ist eine Funktion, die im Nenner x enthält, in der aber keine Wurzel, keine Exponentialfunktion, kein Logarithmus, kein Betrag oder gar Sinus, Kosinus bzw. Tangens vorkommt. Im Zähler kann x vorkommen, muss aber nicht.

Beispiel einer gebrochenrationalen Funktion:

Man unterscheidet zwischen echtgebrochenrationalen und unechtgebrochenrationalen Funktionen.

Bei echtgebrochenrationalen Funktionen ist der Zählergrad (höchste x-Potenz des Zählers) immer kleiner als der Nennergrad (höchste x-Potenz des Nenners).

Bei unechtgebrochenrationalen Funktionen ist der Zählergrad größer oder gleich dem Nennergrad.

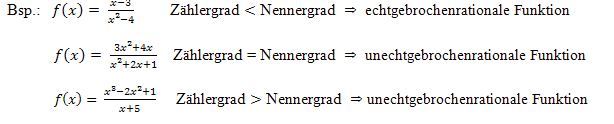
Mehr zu diesem Thema im Bereich Analysis im Kapitel Gebrochenrationale Funktionen.

---