Funktionenschar

So wie eine Schar von Kindern viele Kinder darstellt, so ist eine Funktionenschar nichts anderes als viele Funktionen, die durch eine gemeinsame Gleichung beschrieben sind. Du erkennst eine Funktionenschar daran, dass in der Funktionsgleichung neben der Variablen x auch noch mindestens ein anderer Buchstabe, z.B. a, k oder t, vorkommt. Diese Buchstaben nennt man Scharparameter, kurz Parameter.

Beispiel einer Funktionenschar: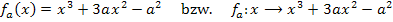

In diesem Beispiel ist der Scharparameter mit a bezeichnet;die Variable ist x.

Die Variable ist meistens mit x bezeichnet;alle anderen in der Funktionsgleichung auftretenden Buchstaben sind die Parameter. Es kann aber auch einmal anders sein. So kann zum Beispiel t an Stelle von x die Variable sein und nicht der Parameter. Das ist vor allem in Aufgaben mit physikalischem Zusammenhang der Fall, da t normalerweise für die Zeit (engl. time) steht.

Woher weißman nun, welcher Buchstabe für die Variable steht und welcher für den Parameter? Ok, meistens ist x die Variable, aber eben nicht immer! Die Variable steht aber im Funktionsterm immer in der Klammer direkt hinter der Benennung der Funktion oder vor dem Pfeil in der Abbildungsvorschrift. Derjenige Buchstabe, der in der Klammer direkt hinter dem f bzw. vor dem Pfeil steht, ist daher die Variable. So kannst du sofort erkennen, was die Variable ist. Der Parameter wird dagegen in der Regel als Index, d.h. kleiner geschriebene, tiefergesetzte Zahl geschrieben. (Manchmal fehlt der Index leider auch.) Dadurch ist klar, welcher Buchstabe die Variable und welcher der Parameter ist.

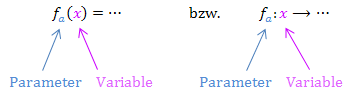
Achtung:Unterscheide genau zwischen der Variablen und dem Parameter. Eine Variable ist, wie der Name schon sagt, eine variable Zahl. Ein Parameter ist dagegen eine konstante Zahl, also eine feste Zahl, die man bloßnicht kennt. In der Schule untersucht man ausschließlich Funktionen mit einer Variablen. Daher kommt auch bei den Funktionenscharen immer nur eine Variable vor. Parameter kann es dagegen auch mehrere Verschiedene geben. Man sagt, es ist eine einparametrige Funktionenschar, wenn nur ein Parameter vorkommt. Eine zweiparametrige Funktionenschar enthält zwei Parameter, eine dreiparametrige Schar entsprechend drei usw.

Beispiel für eine dreiparametrige Funktionenschar: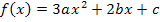

In diesem Beispiel ist wieder x die Variable;a, b und c stellen die Parameter dar.

Hauptsächlich rechnet man in der Schule mit einparametrigen Funktionenscharen.

Will man den Graph einer bestimmten Funktion einer Schar zeichnen, muss man den (bzw. die) Scharparameter kennen. Alle Funktionen der Schar gemeinsam lassen sich nicht zeichnen;nur einzelne Kurven der Schar für bestimmte Werte des Parameters können gezeichnet werden. Heißt es beispielsweise in einer Aufgabe, zeichne den Graph 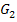der Funktionenschar 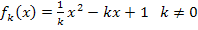, dann bedeutet dies, dass der Scharparameter k = 2 ist. Man setzt dazu für den Parameter k den Wert 2 in die Gleichung der Funktionenschar ein und kann den Graph beispielsweise mit einer Wertetabelle zeichnen. Daran sieht man nun deutlich den Unterschied zwischen Variable und Parameter:Der Parameter ist mit k = 2 festgelegt, für die  Variable x werden in der Wertetabelle verschiedene Zahlen eingesetzt, um die jeweiligen y-Koordinaten zu berechnen. Der Parameter ist also eine feste Zahl, zumindest solange man eine bestimmte Funktion der Schar untersucht, während die Variable alle Zahlen der Definitionsmenge durchläuft.

An die waagrechte Achse des Koordinatensystems schreibt man die Bezeichnung der Variablen. (Wenn die Variable x heißt, ist die waagrechte Achse die x-Achse, so wie du das normalerweise immer machst. Wenn die Variable aber z.B. t heißt, ist die waagrechte Achse entsprechend die t-Achse.) Der Scharparameter hat mit der Achsenbenennung nichts zu tun.

Wenn du mit Funktionenscharen zu tun hast, wirst du immer wieder über die Formulierung „in Abhängigkeit von a oder k (oder einem anderen Buchstaben, der jeweils für den Scharparameter steht)“ stolpern. In Abhängigkeit vom Parameter rechnen, bedeutet, dass man nichts für den Parameter einsetzen soll, sondern einfach mit dem Parameter rechnen soll, als wäre er eine konkrete Zahl. Im Ergebnis kann der Parameter noch vorkommen, muss jedoch nicht. Wenn der Parameter im Ergebnis nicht mehr auftritt, dann heißt das, dass das Ergebnis für alle Funktionen der Schar gilt. Man sagt:Das Ergebnis ist unabhängig vom jeweiligen Scharparameter.

Beispiel: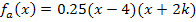

Wir berechnen die Nullstellen der Funktionenschar 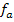in Abhängigkeit von a.

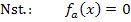
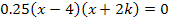
Man kann die Lösungen der Gleichung sofort ablesen. Ein Produkt ist bekanntlich gleich Null, wenn einer der Faktoren gleich Null ist. Man kann also die Faktoren einzeln gleich Null setzen. Der erste Faktor ist die Zahl 0,25. Sie kann gar nicht gleich Null werden. Die erste Klammer 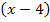ergibt Null, wenn man für x die Zahl 4 einsetzt. Die zweite Klammer wird gleich Null, wenn man für x den Ausdruck -2k einsetzt.

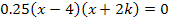
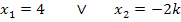
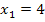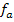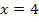Die erste Nullstelle ist unabhängig vom Parameter k. (Es kommt kein k in dieser Lösung vor.) D.h., dass alle Funktionen der Schar bei eine Nullstelle haben. Jede Funktion der Schar 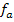verläuft durch den Punkt 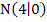. Es handelt sich um eine gemeinsame Nullstelle aller Funktionen dieser Schar. Der Punkt 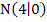ist gemeinsamer Punkt aller Funktionen der Schar.

Die zweite Nullstelle 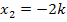ist abhängig vom Parameter k. (Es kommt k in dieser Lösung vor.) Alle Scharfunktionen haben somit verschiedene zweite Nullstellen. Je nach dem, was für k eingesetzt wird, erhält man nämlich ein anderes Ergebnis. Jede Funktion der Schar 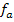verläuft durch einen anderen Punkt .

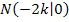Zusammenfassend lässt sich sagen, dass alle Funktionen der Schar 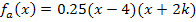die x-Achse bei 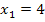schneiden, aber dass sie die x-Achse jeweils auch bei 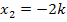schneiden, was jedoch von k abhängt. Einen Sonderfall stellt außerdem 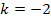dar, denn für 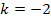fallen die Nullstellen 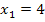und 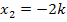zu einer doppelten Nullstelle zusammen. Für 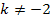hat die Scharfunktion zwei einfache Nullstellen. Für 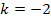ergibt sich nur eine doppelte Nullstelle bei 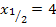. Bei einer einfachen Nullstelle schneidet der Graph die x-Achse;bei einer doppelten berührt er sie nur. Siehe auch:Vielfachheiten der Nullstellen

Man muss hier also die beiden Fälle 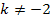und 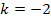unterscheiden. So etwas nennt man Fallunterscheidung. Bei der Kurvendiskussion von Funktionenscharen sind oft Fallunterscheidungen nötig, nicht nur bei der Untersuchung der Nullstellen. Dies macht die Funktionenscharen für Lehrer besonders interessant und für die meisten Schüler zum Problem.

---