Faktorisierter Funktionsterm

Ein Funktionsterm liegt in seiner faktorisierten Form vor, wenn er soweit möglich in Linearfaktoren zerlegt ist. Man kann die faktorisierte Form auch als Produktform bezeichnen. Die einzelnen Faktoren des Produkts nennt man Linearfaktoren, wenn sie die Form ax+b haben, also kein 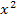oder eine noch höhere Potenz von x enthalten.

Bsp.: 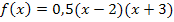faktorisierte Form der Funktion f

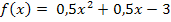ausmultiplizierte Form der Funktion f

Um die faktorisierte Form auf die ausmultiplizierte Form zu bringen, braucht man nur alle Faktoren miteinander zu multiplizieren.

Umgekehrt von der ausmultiplizierten Form auf die faktorisierte Form zu kommen, ist deutlich anspruchsvoller. Das nennt man dann „Faktorisieren“. Bis zur 8. Klasse beschränkt sich dies auf reines Ausklammern. Ab der 9. Klasse musst du , zumindest bei quadratischen Funktionen, auch faktorisieren können, wenn sich x nicht einfach ausklammern lässt. Ende der 10. Klasse wird im Schulunterricht allerdings nur im Gymnasium (G8) auch das Faktorisieren von Polynomen dritten und höheren Grades behandelt, d.h. das Zerlegen in Linearfaktoren bei Funktionen mit 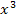und höheren Potenzen. Auch für Schüler der 11. Klasse einer FOS/BOS ist dies Stoff.

Das Zerlegen der ausmultiplizierten Form in die einzelnen Linearfaktoren, nennt man wie gesagt „Faktorisieren“. Je nach Art des Funktionsterm kann faktorisiert werden, indem man ausklammert, binomische Formeln oder eventuell den Satz von Vietaanwendet.

1. Bsp.:

Faktorisiere die folgenden Funktionsterme vollständig!

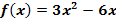
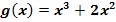
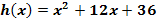(nur für Schüler ab der 9. Klasse)

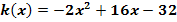(nur für Schüler ab der 9. Klasse)

Lösung:

Bei der Funktion 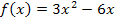lässt sich sowohl die Zahl 3 als auch x ausklammern. So erhält man:

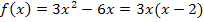
Dies ist bereits die vollständig faktorisierte Form. Fertig!

Bei der Funktion 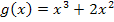kann der Faktor ausgeklammert werden.

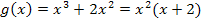
In der Gleichung der Funktion 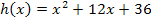ist die erste binomische Formel versteckt.

Zur Erinnerung:

1. binomische Formel

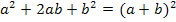
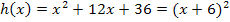
Bei der Funktion 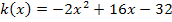musst du zuerst den Faktor -2 ausklammern. Danach müsste dir eigentlich etwas auffallen. Was, das wird noch nicht verraten. Du kommst vermutlich auch alleine darauf. Jetzt klammern wir erst ´mal aus:

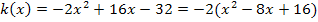
So, was ist nun mit der Klammer? Hast du es erkannt? Richtig, wieder ein Binom, aber dieses Mal ist es die 2. binomische Formel.

Zur Erinnerung:

2. binomische Formel

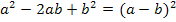
Wende sie doch gleich alleine an!

Wenn du richtig gerechnet hast, bist du zu folgendem Ergebnis gekommen:

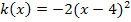
Für Schüler ab der 9. Klasse:

Was macht man aber, wenn sich kein x ausklammern lässt und auch keine binomische Formel angewendet werden kann? Hm? Das ist jetzt nicht mehr ganz so einfach. Da muss man wirklich wissen, wie das geht. Selber d´rauf kommen, ist echt schwer.

Merke:

Falls Ausklammern und binomische Formeln nicht funktionieren, hilft es den zu faktorisierenden Funktionsterm gleich Null zu setzen und die Gleichung z.B. mit der Mitternachtsformel bzw. bei Gleichungen mit 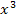oder höheren Potenzen mit Hilfe einer Polynomdivisionauszurechnen. Es gibt dann genauso viele Linearfaktoren wie Lösungen der Gleichung.

---