Extrema/Extrempunkte

Zu den Extrema oder Extrempunkten zählt man die Maxima und Minima einer Funktion. Es handelt sich dabei um die Punkte mit den größten bzw. kleinsten Funktionswerten, entweder insgesamt oder nur in einer bestimmten Umgebung. Die zugehörigen Punkte auf dem Graph der Funktion werden als Hochpunkte (HOP) bzw. Tiefpunkte (TIP) bezeichnet. Man unterscheidet relative und absolute Extrema. Ein relatives Extremum liegt nur lokal, also in einer bestimmten Umgebung, am höchsten bzw. tiefsten. Dagegen ist ein absolutes Extremum wirklich der absolut höchste bzw. tiefste Punkt des Graphen.

Um die Extrempunkte einer in ihren gesamten Definitionsmenge differenzierbaren Funktion f(x) zu ermitteln, setzt man zuerst die erste Ableitung f´(x) gleich Null, da bei jedem Extremum die Tangentean den Graph der Funktion waagrecht verläuft und somit dort die Steigung, also f´(x), gleich Null sein muss.

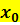Extremum: f´( ) = 0

Das ist allerdings nur eine notwendige Bedingung für ein Extremum, d.h. es kann an der Stelle 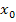ein Extremum vorliegen, muss aber nicht. Es könnte sich auch um einen sogenannten Terrassenpunkt (kein Extremum!) handeln, weil auch bei Terrassenpunkten die Tangente waagrecht verläuft. In anderen Worten:Bei jedem Extremum liegt zwar eine waagrechte Tangente vor, aber nicht bei jedem Punkt mit waagrechter Tangente handelt es sich um ein Extremum! Mit dem Ansatz  f´( 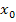) = 0 werden die x-Koordinaten aller Punkte mit waagrechter Tangente ermittelt, also der Extrema, aber auch der Terrassenpunkte.

Um nachzuweisen, dass wirklich ein Extremum vorliegt, benötigt man noch eine weitere Bedingung, die sogenannte hinreichende Bedingung. Dabei gibt es zwei verschiedene Möglichkeiten:Entweder verwendet man die zweite Ableitung f´´(x) und zeigt, dass sie an der Stelle 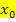nicht gleich Null ist, oder man untersucht das Steigungsverhalten, die Monotonie, der Funktion. Da die zweite Ableitung f´´(x) im G8 erst in der 12. Klasse auf dem Lehrplan steht, musst du, solange du f´´(x) noch nicht gelernt hast, mit Hilfe der Monotonie nachweisen, dass es sich bei dem Punkt mit waagrechter Tangente wirklich um einen Extrempunkt handelt.

Damit sicher ein Extremum vorliegt, muss sich das Monotonieverhalten ändern. Die Voraussetzung für ein relatives Extremum ist daher ein Vorzeichenwechsel der ersten Ableitung, d.h. des Steigungsverhaltens. Die Steigung des Graphen 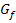berechnet man schließlich mit Hilfe der ersten Ableitung f´(x). Ändert sich das Vorzeichen der ersten Ableitung f´(x) an der Stelle 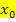, liegt an dieser Stelle sicher ein Extremum vor. Ändert sich dagegen das Vorzeichen der Ableitung nicht, liegt bei 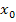ein Terrassenpunkt, d.h. kein Extremum, vor.

Mit Hilfe der Monotonie kann nicht nur nachgewiesen werden, dass an einer bestimmten Stelle 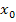ein Extremum vorliegt, sondern es kann auch zwischen relativen Maxima und relativen Minima unterschieden werden.

Wenn der Graph zuerst steigt (positive Steigung f´(x)) und dann fällt (negative Steigung f´(x)), hat der Graph einen relativen Hochpunkt, kurz HOP.

Monotonietabelle:

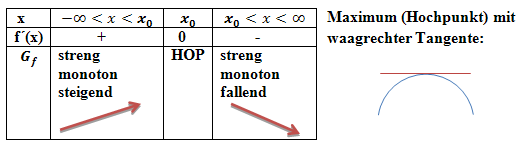
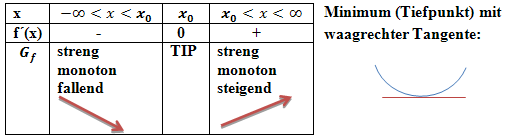
Wenn umgekehrt der Graph zuerst  fällt (negative Steigung) und dann steigt (positive Steigung), liegt ein relativer Tiefpunkt, kurz TIP, vor.

Mehr zum Thema Extrema findest du im Bereich Analysis in den Kapiteln Erste Ableitung f´(x) und Kurvendiskussion.