Ergebnisraum Ω

Unter dem Ergebnisraum 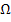 (Sprich:„Omega“) versteht man in der Wahrscheinlichkeits-rechnung die Menge aller möglichen Fälle, die sich bei einem Zufallsexperiment ergeben können. Jede einzelne Möglichkeit bezeichnet man als Elementarereignis. Der Ergebnisraum  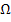ist daher die Menge aller Elementarereignisse.

Unter der Mächtigkeit des Ergebnisraums 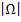 (Sprich:„Betrag von Omega“) versteht man die Anzahl aller möglichen Fälle, also die Anzahl aller Elementarereignisse eines Zufallsexperiments.  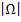gibt daher an, wie viele verschiedene Fälle herauskommen können.

Beispiele:

Einmaliges Werfen eines Würfels

Der Würfel kann die Augenzahlen 1, 2, 3, 4, 5 oder 6 zeigen. Deshalb lautet der Ergebnisraum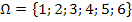

Es gibt 6 verschiedene Elementarereignisse, d.h. 6 verschiedene Möglichkeiten. Daher gilt für die Mächtigkeit des Ergebnisraums:

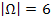
Zweimaliges Werfen einer Münze (unter Beachtung der Reihenfolge)

Auf der einen Seite der Münze ist ein Wappen W, auf der anderen Seite eine Zahl Z. Wird diese Münze zweimal nacheinander geworfen, gibt es die folgenden verschiedenen Fälle:

Zweimal Wappen WW

Zuerst Wappen, dann Zahl WZ

Zuerst Zahl, dann Wappen ZW

Zweimal Zahl ZZ

Daher lautet der Ergebnisraum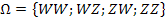

Es gibt also 4 Elementarereignisse, d.h. 4 verschiedene mögliche Fälle. Daher gilt für die Mächtigkeit des Ergebnisraums:

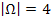
Um etwas größere Ergebnisräume zu ermitteln, zeichnet man sich oft auch ein sogenanntes Baumdiagramm und liest daraus alle möglichen Elementarereignisse ab. Mit Hilfe der Kombinatorik kann die Mächtigkeit eines Zufallsexperiments direkt berechnet werden, ohne vorher den Ergebnisraum anzugeben. Das ist vor allem wichtig für die Berechnung von Laplace-Wahrscheinlichkeiten.

Mehr zu diesem Thema findest du im Bereich Stochastik im Kapitel Ergebnisraum 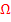 und Mächtigkeit des Ergebnisraums