Ereignis

Als Ereignis bezeichnet man in der Stochastik eine Teilmenge des Ergebnisraums 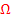. Ein Ereignis kann mit Worten oder als Menge mit geschweiften Klammern geschrieben werden. Oft werden Ereignisse auch mit Großbuchstaben bezeichnet.

Beispiel:Eine Münze wird zweimal geworfen. Gib den Ergebnisraum 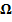und alle Elemente der folgenden, in Worten gegebenen Ereignisse in aufzählender Mengenschreibweise an!

A = „Genau zweimal Wappen“

B = „Mindestens einmal Zahl“

C = „Dreimal Zahl“

D = „Höchstens zweimal Wappen“

E = „Höchstens einmal Wappen“

Lösung:

Der Ergebnisraum enthält alle möglichen Fälle.

Ergebnisraum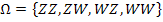

A = „Genau zweimal Wappen“ A =

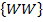
B = „Mindestens einmal Zahl“ B =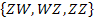

C = „Dreimal Zahl“ C =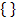

D = „Höchstens zweimal Wappen“    D = =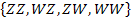

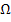
E = „Höchstens einmal Wappen“ E =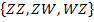

Anmerkung:

Das Ereignis C enthält kein Element, es entspricht also der leeren Menge, da es bei einem zweimaligen Wurf einer Münze gar nicht möglich ist, dreimal eine Zahl zu werfen. Es handelt sich hier um ein unmögliches Ereignis.

Das Ereignis D entspricht dem Ergebnisraum 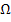;es tritt mit 100% Wahrscheinlichkeit, also ganz sicher ein, da bei einem zweimaligen Wurf einer Münze Wappen höchstens zweimal auftreten kann. Bei D handelt es sich daher um ein sicheres Ereignis.

Das Ereignis E ist das sogenannte Gegenereignis zu Ereignis A, da E genau die Elemente des Ergebnisraums 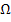enthält, die nicht in A enthalten sind. Statt E könnte man auch Nicht-A sagen. Das Gegenereignis zu A wird durch einen waagrechten Strich über dem A ausgedrückt.

E = 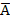(Sprich:„ Nicht-A“)

Umgekehrt ist auch A das Gegenereignis zu E.

A =