Elementarereignis

Ein Elementarereignis ist ein Ereignis, also eine Teilmenge des Ergebnisraumes 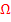, das nur ein einzelnes Element besitzt. Alle möglichen Elementarereignisse ergeben zusammen wieder den Ergebnisraum 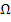, wobei jedes Elementarereignis genau einmal in 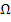vorkommt. Ein Elementarereignis ist also nichts anderes als ein möglicher Ausgang eines Zufallsexperiments. Gibt es bei einem Zufallsexperimentn verschiedene mögliche Ausgänge, dann gibt es auch n verschiedene Elementarereignisse.

Die einzelnen Elementarereignisse werden mit 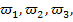… bezeichnet. Man kann jedes Elementarereignis jeweils mit Worten beschreiben oder als Menge (mit genau einem Element) angeben, dabei werden, wie bei Mengen in aufzählender Form üblich, geschweifte Klammern verwendet. Vergleiche dazu folgendes Beispiel!

Beispiel:Einmaliges Werfen eines Würfels (Normaler Würfel mit den Augenzahlen von Eins bis Sechs)

Da es sich um einen gewöhnlichen Würfel handelt, können die Augenzahlen 1, 2, 3, 4, 5 und 6 geworfen werden. Der Ergebnisraum 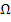enthält bekanntlich alle möglichen Ergebnisse. Deshalb gilt für den Ergebnisraum in diesem Beispiel: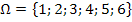

Der Ergebnisraum 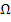enthält also sechs verschiedene Elementarereignisse:

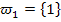In Worten:„Augensumme 1“

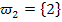In Worten:„Augensumme 2“

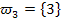In Worten:„Augensumme 3“

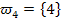In Worten:„Augensumme 4“

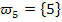In Worten:„Augensumme 5“

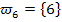In Worten:„Augensumme 6“

Gegenbeispiel:Das Ereignis A = „Gerade Augensumme“  bzw. A = 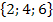ist kein Elementarereignis, da es drei Elemente enthält. Ein Elementarereignis enthält laut Definition genau ein Element, nicht mehr und nicht weniger.

Mehr zu diesem Thema findest du im Bereich Stochastik in den Kapiteln Ergebnisraum und Mächtigkeit des Ergebnisraums und Ereignis, Ereignisraum und Mächtigkeit des Ereignisraums