Dreimal-Mindestens-Aufgabe

Es handelt sich hierbei um einen in der Stochastik/Wahrscheinlichkeitsrechnung häufig gestellten Aufgabentyp. Die Bezeichnung „Dreimal-Mindestens-Aufgabe“ ist keine offizielle mathematische Bezeichnung. Sie wird dennoch von vielen Lehrern für folgenden Aufgabentyp verwendet, da das Wort „mindestens“ dreimal in der Aufgabenstellung vorkommt.

Wie oft muss ein Versuch mindestens durchgeführt werden, damit mit einer Wahrscheinlichkeit von mindestens … %  mindestens ein Treffer kommt? (Die Wahrscheinlichkeit für einen einzelnen Treffer beträgt dabei konstant p und ist in der Aufgabenstellung gegeben.) Gesucht ist also die Anzahl der Versuche;sie wird mit n bezeichnet.

Lösungsansatz:

Ges.:Anzahl der Versuche n

X steht für die Anzahl der Treffer

Geg.:Trefferwahrscheinlichkeit p      Nietenwahrscheinlichkeit q = 1 – p

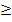P(X 1) … %

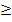1 – P(X = 0) … %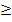

1 … %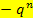

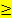Nach der Unbekannten n wird letztendlich mit Hilfe des Logarithmus aufgelöst, da n im Exponenten steht. Wenn du ein konkretes Beispiel für eine Dreimal-Mindestens-Aufgabe suchst, gehe in den Bereich Stochastik zum Kapitel Stochastisch unabhängige Ereignisse Bsp.5 oder zum Kapitel Bernoulli-Kette und Binomial-Verteilung.

Mit einem entsprechenden Ansatz können auch Aufgaben gelöst werden, in denen p gesucht, aber n gegeben ist. Dann verwendet man anstelle von q jedoch besser 1 – p im Lösungsansatz, da sonst die gesuchte Größe p gar nicht vorkommt.

1 … %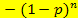

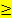Am Ende der Rechnung muss die n.te Wurzel 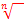gezogen werden, um nach p aufzulösen, weil das gesuchte p in der Basis vorkommt, und nicht wie n im Exponenten. Hier also keinen Logarithmus verwenden!