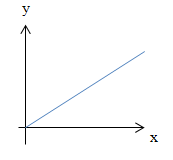Direkte Proportionalität
Es geht hierbei um den Zusammenhang zweier verschiedener Größen x und y. Zwei Größen x und y sind direkt proportional zueinander, wenn sich bei einer Ver-n-fachung der einen Größe x auch die zweite Größe y ver-n-facht. Einfacher gesagt:Halbiert man x, halbiert sich auch y. Verdoppelt man x, so verdoppelt sich auch y. Verdreifacht man x, so verdreifacht sich auch y. Entsprechend vervierfacht sich y, wenn man x vervierfacht usw., x und y verhalten sich also entsprechend. Man sagt:Es liegt eine direkte Proportionalität zwischen den beiden Größen x und y vor.
Beispiel:
Wir kaufen jeden Morgen beim selben Bäcker die gleichen Semmeln. Der Preis einer Semmel soll immer gleich bleiben, beispielsweise 0,35 € pro Semmel.
x ist die Anzahl der gekauften Semmeln und y der Preis in €, den man für die Semmeln insgesamt bezahlen muss. Kauft man doppelt so viele Semmeln, d.h. man verdoppelt die Anzahl x der gekauften Semmeln, dann verdoppelt sich auch der insgesamt zu bezahlende Preis y. Die Anzahl x der Semmeln verhält sich direkt proportional zum Preis y der gekauften Semmeln.
Das mathematische Zeichen für „direkt proportional“ ist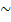 
. Um mathematisch auszudrücken, dass die beiden Größen x und y direkt proportional zueinander sind, schreibt man:x 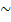y
| Für zwei direkt proportionale Größen x und y gilt:
· Sie sind quotientengleich, d.h. der Quotient · Die Zahl k heißt Proportionalitätsfaktor oder auch Proportionalitätskonstante. · Die Abbildungsvorschrift (=Zuordnungsvorschrift) der direkten Proportionalität lautet allgemein:
· Alle Wertepaare (x|y) liegen auf einer Halbgerade durch den Ursprung:
|
nimmt für alle Wertepaare x und y den gleichen Wert k an.
In unserem Beispiel von oben könnte man z.B. folgende Wertetabelle erstellen:
| Anzahl der Semmeln x | 0 | 1 | 2 | 3 | 4 | 10 |
| Preis y in € | 0,00 | 0,35 | 0,70 | 1,05 | 1,40 | 3,50 |
Rechnerischer Nachweis der direkten Proportionalität mit Hilfe der Quotientengleichheit:
Abgesehen vom Wertepaar (0|0), bei dem der Quotient 
nicht berechnet werden kann, da hier der Nenner gleich Null werden würde und somit nicht definiert wäre, ergeben alle Quotienten den gleichen Wert.
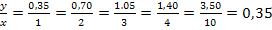
Die Wertepaare sind quotientengleich. Dadurch ist rechnerisch nachgewiesen, dass die Anzahl der gekauften Semmeln x direkt proportional zum Preis y (in €) der gekauften Semmeln ist.
Der Proportionalitätsfaktor k:
Das Ergebnis des Quotienten ergibt den Proportionalitätsfaktor k. In diesem Beispiel ist der Proportionalitätsfaktor k die Zahl 0,35. Es gilt hier also:k = 0,35
Der Proportionalitätsfaktor k hat auch eine anschauliche Bedeutung. Das hängt natürlich vom Sachzusammenhang ab. Auf jeden Fall gibt k immer den y-Wert zum x-Wert 1 an.
In unserem Beispiel gibt k also den Preis für eine einzelne Semmel an:Eine Semmel kostet 0,35 €. (Das war hier natürlich schon im Text gegeben, doch oft wird in anderen Aufgaben genau nach der Bedeutung von k im jeweiligen Zusammenhang gefragt.)
Die Abbildungs- bzw. Zuordnungsvorschrift:
Die Abbildungs- bzw. Zuordnungsvorschrift, welche der Anzahl x der gekauften Semmeln den Preis y in € zuordnet, lautet: x 
y = 0,35x
bzw. x 0,35x
Um diese Abbildungsvorschrift zu erhalten, muss der vorher berechnete Wert von k in die allgemeine Abbildungsvorschrift (=Zuordnungsvorschrift) der direkten Proportionalität x y = kx bzw. x kx eingesetzt werden.
Wenn in einer Aufgabe eine der beiden Größen x oder y gegeben ist und der zugehörige zweite Wert gefragt ist, musst du bloßden gegebenen Wert für x bzw. y in die Abbildungsvorschrift dieser Zuordnung einsetzen und eventuell noch nach dem gesuchten Wert auflösen. Dazu brauchst du natürlich die Abbildungsvorschrift dieser Zuordnung. Sind alle Wertepaare quotientengleich, weißt du, dass eine direkt proportionale Zuordnung vorliegt. Das Ergebnis der Quotienten = k kannst du für k in die allgemeine Abbildungsvorschrift y = kx einsetzen. Dann hast du die Abbildungsvorschrift dieser speziellen direkt proportionalen Zuordnung.
Nun kannst den gegebenen Wert, z.B. x, in diese Abbildungsvorschrift einsetzen und den zugehörigen Wert y leicht ausrechnen.
Graph einer direkt proportionalen Zuordnung:
Ist die Abbildungsvorschrift bekannt, kann man den Graph ganz leicht zeichnen. Man weißja, dass alle Wertepaare einer direkt proportionalen Zuordnung immer auf einer Halbgerade durch den Ursprung liegen. Das ist eine „Gerade“, die im Ursprung beginnt. Eine echte Gerade hat weder Anfang noch Ende. Da die x-Werte einer direkt proportionalen Zuordnung immer positiv sind, kann der Graph nur rechts von der y-Achse verlaufen. Warum x nicht negativ sein kann, wird dir bestimmt schon in unserem Beispiel klar:x stellt hier die Anzahl der gekauften Semmeln dar;eine Anzahl kann aber gar nicht negativ sein. Entweder man kauft überhaupt welche, dann ist x positiv, oder man kauft eben keine Semmel, dann ist x = 0. Für x = 0 ergibt sich immer y = 0. Auf unser Beispiel bezogen:0 Semmeln (x = 0) kosten schließlich 0 € (y = 0). Daher beginnt der Graph immer im Ursprung.
In unserem Beispiel kann x auch nur natürliche Zahlen annehmen, da man schließlich keine halben oder viertel Semmeln kaufen kann. Der Graph besteht daher in diesem Beispiel nur aus einzelnen Punkten, die alle auf einer Halbgeraden durch den Ursprung liegen. In anderen Aufgaben kann x allerdings auch Dezimalzahlen annehmen, z.B. wenn x für eine Zeit steht. Dann ist der Graph eine (durchgezogene) Halbgerade. Wir wissen dann, dass der Graph im Ursprung beginnt. Nun braucht man eigentlich nur noch einen weiteren Punkt und man kann die Halbgerade zeichnen. Also berechnet man, wie gerade erklärt, ein Wertepaar (x|y). Dieses Wertepaar zeichnest du als zweiten Punkt der Halbgerade ein. Jetzt kann der Graph bequem gezeichnet werden.
An Stelle der Berechnung eines Wertepaares als zweiten Punkt, kannst du auch einen kleinen Trick anwenden:Die Halbgerade verläuft auch immer durch den Punkt (1|k), wobei k wieder der Proportionalitätsfaktor ist. D.h. du liest k aus der Abbildungsvorschrift ab, zumindest wenn sie gegeben ist, und zeichnest die Halbgerade mit Hilfe des Punktes (1|k) und dem Ursprung.
Hast du schon eine Wertetabelle vorliegen, kannst du natürlich auch einfach diese Wertepaare verwenden und sie als Punkte in ein Koordinatensystem einzeichnen. Handelt es sich um eine direkt proportionale Zuordnung, müssen alle Punkte auf einer Halbgeraden durch den Ursprung liegen. Ob du die einzelnen Punkte dann noch zu einer Halbgeraden verbindest oder nicht, hängt davon ab, ob x nur natürliche Zahlen oder auch Dezimalzahlen annehmen kann.
Wenn du ausführlichere Erläuterungen zur direkten Proportionalität suchst, gehe in den Bereich Analysis in das Kapitel Direkte und indirekte Proportionalität, dort wird alles noch einmal mit vielen Beispielen erklärt.
Von der direkten Proportionalität ist die Indirekte Proportionalität, auch umgekehrte Proportionalität genannt, zu unterscheiden. Wie der Name schon sagt, verhalten sich hierbei x und y genau umgekehrt zueinander:Verdoppelt man x, so halbiert sich y. Verdreifacht sich x, so wird y gedrittelt usw. Verdoppelt man beispielsweise die Anzahl x der Arbeiter, die eine bestimmte Arbeit verrichten sollen, so halbiert sich die dafür benötigte Zeit y.
Die Zuordnung Anzahl der Arbeiter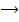 
benötigte Zeit für eine bestimmte Arbeit ist indirekt proportional, zumindest dann, wenn wir davon ausgehen, dass alle Arbeiter gleich effektiv arbeiten und sich die Arbeitsleistung durch die Zusammenarbeit mehrerer Arbeiter weder verbessert noch verschlechtert.
