Differenzierbarkeit/Differenzierbare Funktion
Eine Funktion f ist differenzierbar, wenn ihr Graph keine Knicke oder Spitzen aufweist. Der Graph einer in ihrer ganzen Definitionsmenge differenzierbaren Funktion verläuft also überall „weich“ bzw. „glatt“. Die Steigung der Funktion lässt sich in jedem Kurvenpunkt P berechnen. Die Steigung der Funktion f im Punkt P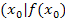 
) entspricht dabei der Steigung der Tangente an den Graph 
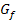im Punkt P ).
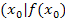Hinweis:Mit 
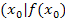ist eine bestimmte Zahl gemeint. P ) ist daher ein festgelegter Punkt des Graphen.
Kann die Steigung der Funktion, also die Tangentensteigung, in einem bestimmten Punkt nicht angegeben werden, weil sie an dieser Stelle einen Knick hat, sagt man:Die Funktion ist an dieser Stelle nicht differenzierbar.
Hat der Graph der Funktion an einer bestimmten Stelle eine Sprungstelle, d.h. sie ist an dieser Stelle nicht stetig, kann die Steigung dort natürlich auch nicht angegeben werden. Daher ist die Stetigkeit an der Stelle absolute Voraussetzung für die Differenzierbarkeit bei . Damit eine Funktion an der Stelle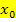 
überhaupt differenzierbar sein kann, muss sie an der Stelle 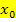erst einmal stetig sein.
Merke:Immer zuerst überprüfen, ob die Funktion an der Stelle 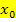stetig ist, bevor man die Differenzierbarkeit an der Stelle 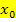untersucht!
Ist die Funktion nämlich bei gar nicht stetig, dann kann man sich die Untersuchung auf Differenzierbarkeit komplett schenken, weil die Funktion dann an der Stelle sowieso nicht differenzierbar sein kann.
nicht stetig bei 
nicht differenzierbar bei
Vorsicht:Eine an der Stelle nicht differenzierbare Funktion kann dort stetig sein oder auch nicht! Von der Aussage „nicht differenzierbar“ kann also nicht sofort auf die Stetigkeit geschlossen werden. Allerdings ist jede differenzierbare Funktion zwangsläufig stetig, da die Stetigkeit eine Voraussetzung für die Differenzierbarkeit ist.
differenzierbar bei 
stetig bei
Jetzt bitte nicht erschrecken! Die folgende Definition sieht ziemlich kompliziert aus, wird aber danach gleich noch erklärt.
| Definition: Eine an der Stelle stetige Funktion f(x) ist an der Stelle differenzierbar, wenn gilt:
|
Anmerkung:
ist eine konkrete Zahl. Eine Funktion wird immer lokal, also an einer bestimmten Stelle auf Differenzierbarkeit untersucht. Im ersten nachfolgenden Beispiel (siehe unten) ist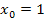 
. Mit ist also die x-Koordinate der zu untersuchende „Problemstelle“ gemeint, an der die jeweiligen Teilfunktionen einer teilweise definierten Funktion zusammenstoßen.
