Definitionslücke
Eine einzelne Zahl, für die ein Term oder eine Funktion nicht definiert ist, nennt man Definitionslücke. Es gibt zwei verschiedene Arten von Definitionslücken:Die stetig fortsetzbaren Definitionslücken, die im Graph wie Löcher aussehen, und die sogenannten Polstellen (kurz:Pole), an denen der Graph nach oben bzw. unten ins Unendliche schießt. An den Polstellen, manchmal auch als Unendlichkeitsstellen bezeichnet, schmiegt sich der Funktionsgraph an eine senkrechte Gerade an. Diese Gerade wird als senkrechte Asymptote bezeichnet. Der Graph nähert sich ihr immer mehr an, schneidet sie jedoch nie! (Wenn du in die Mittelstufe gehst, wirst du fast nur mit Polstellen bzw. senkrechten Asymptoten zu tun haben. Löcher werden erst in der Oberstufe wichtig.)
Bei gebrochenrationalen Funktionen lässt sich am faktorisierten Funktionsterm leicht erkennen, welche Art von Definitionslücke vorliegt:
| „Loch“(=Stetig fortsetzbare oder auch stetig behebbare Definitionslücke) | Polstellebzw. Unendlichkeitsstelle
(= Senkrechte Asymptote, d.h. senkrechte Gerade, an die sich |
|
|
| vollständig aus dem Nenner wegkürzbar | nicht (vollständig aus dem Nenner) wegkürzbar |
Stetige Fortsetzung: 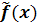
= gekürztes
Bsp.:
Die Definitionslücke x = 3 ist ein Loch, da sie aus dem Nenner vollständig weggekürzet werden kann. Durch das Kürzen „verliert“ man allerdings diese Definitionslücke, daher darf genaugenommen nicht mehr die Schreibweise f(x) für die gekürzte Funktion verwendet werden, man sollte die Schreibweise mit der „Schlange über dem f“ verwenden:
Wenn man die Definitionsmenge der stetigen Fortsetzung Die Definitionslücke x = 1 ist dagegen erhalten geblieben. Sie ist ein Pol, da sie nicht wegkürzbar ist.(Siehe rechte Spalte!) |
Gleichung der senkrechten
Asymptote:
Bsp.:
Die Definitionslücke x = 1 ist nicht wegkürzbar, daher liegt ein Pol vor. Die Gleichung der senkrechten Asymptote lautet:
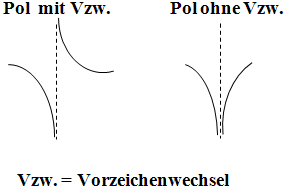
Es handelt sich um einen Pol mit Vorzeichenwechsel:Der Graph geht also einmal gegen Unterscheidung zwischen Pol mit bzw. ohne Vorzeichenwechsel:
Pol ungerader Ordnung: mit Vzw. Pol gerader Ordnung: ohne Vzw.
Liegt die Funktion in der faktorisierten (falls möglich gekürzten) Form vor, dann erkennt man die Ordnung des Pols an der Potenz außerhalb der Klammer der jeweiligen Polstelle.
|
| y-Koordinate des „Lochs“ berechnen:
Definitionslücke in gekürzte Form von f(x), also in
bzw. ab 11.Klasse:Grenzwert berechnen:
Sprich: „Limes von x gegen (wobei
Bsp.:
Das Loch hat die x-Koordinate x = 3. Die y-Koordinate des Lochs berechnet man, wie im Folgenden dargestellt:
Das Loch hat die Koordinaten L(3;2,5)
|
1. Bsp.: 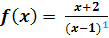 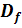 = = 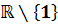
Wie schon oben erwähnt, liegt an der Stelle x = 1 ein Pol mit Vorzeichenwechsel vor, da es sich um einen Pol 2. Bsp.:
In diesem Beispiel liegt an der Stelle x = 3 ein Pol ohne Vorzeichenwechsel vor, da es sich um einen Pol 3. Bsp.:
Diese Funktion hat zwei verschiedene Polstellen: Die erste Klammer im Nenner wird Null, wenn man x = 1 setzt. Die Klammer ist nicht kürzbar, daher liegt bei x = 1 ein Pol vor. Es handelt sich um einen Pol Die zweite Klammer im Nenner wird Null, wenn man x = -4 setzt. Diese Klammer ist ebenfalls nicht wegkürzbar, deshalb liegt bei x = -4 auch ein Pol vor. Allerdings handelt es sich hier um einen Pol ohne Vorzeichenwechsel, weil es ein Pol Anmerkung: Anstelle „Pol x-ter Ordnung“ wird auch die Bezeichnung „Pol x-ten Grades“ verwendet. Die Potenzen außerhalb der Klammern werden auch „Vielfachheiten“ genannt. |

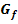 anschmiegt)
anschmiegt)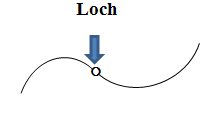
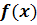
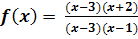
 =
= 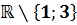
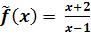
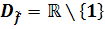
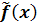 ist die stetige Fortsetzung der Funktion f.
ist die stetige Fortsetzung der Funktion f. 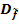 mit der Definitionsmenge der ungekürzten Funktion
mit der Definitionsmenge der ungekürzten Funktion 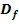 vergleicht, stellt man fest, dass die Definitionslücke bei x = 3 „verlorengegangen“ ist. Das ist bei einem Loch immer der Fall.
vergleicht, stellt man fest, dass die Definitionslücke bei x = 3 „verlorengegangen“ ist. Das ist bei einem Loch immer der Fall.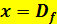
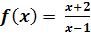
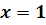
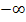 und einmal gegen +
und einmal gegen + 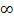 , d.h. auf der einen Seite der senkrechten Asymptote schießt er nach unten und auf der anderen Seite nach oben. (Vergleiche Skizze oben links!)
, d.h. auf der einen Seite der senkrechten Asymptote schießt er nach unten und auf der anderen Seite nach oben. (Vergleiche Skizze oben links!)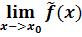
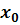 …“
…“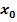 für die wegkürzbare Definitionslücke steht, in diesem Beispiel
für die wegkürzbare Definitionslücke steht, in diesem Beispiel 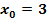 )
)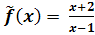
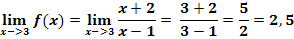
 Ordnung (ungerader Ordnung) handelt. Vergleiche auch Skizze oben links!
Ordnung (ungerader Ordnung) handelt. Vergleiche auch Skizze oben links!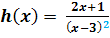
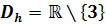
 Ordnung (gerader Ordnung) handelt. Vergleiche auch Skizze oben rechts!
Ordnung (gerader Ordnung) handelt. Vergleiche auch Skizze oben rechts!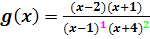
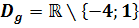
 Ordnung (ungerader Ordnung), deshalb handelt es sich hier um einen Pol mit Vorzeichenwechsel.
Ordnung (ungerader Ordnung), deshalb handelt es sich hier um einen Pol mit Vorzeichenwechsel. Ordnung (gerader Ordnung) ist.
Ordnung (gerader Ordnung) ist.