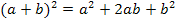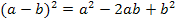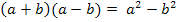Binom/Binomische Formeln
Es gibt drei verschiedene sogenannte binomische Formeln bzw. kurz Binome.
|
1. Binomische Formel: 2. Binomische Formel: 3. Binomische Formel: |
Diese drei Formeln sind in der Algebra sehr wichtig;man braucht sie wirklich immer wieder. Du solltest sie unbedingt auswendig können! Die Bezeichnung „Binom“ kommt übrigens daher, dass in der Klammer immer zwei Faktoren stehen und „bi“ bedeutet ja „zwei“. (Lat. bis = zweimal) In der oben gezeigten Darstellung steht jeweils auf der linken Seite der Gleichungen die sogenannte „Produkt-Form“ und auf der rechten Seite die sogenannte „Summen bzw. Differenzen-Form“ der Binome.
Anmerkung:Ein Quadrat ist ja ein Produkt mit sich selbst. Daher ist nicht nur der Ausdruck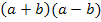 
ein Produkt, sondern auch 
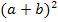und 
.
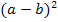In der Summen bzw. Differenzen-Form, also in der oben gezeigten Darstellung auf der rechten Seite, kommt in der ersten und zweiten Binomischen Formel der Ausdruck 2ab vor. Man nennt diesen Ausdruck das gemischte Glied, da er gemischt ist aus a und b. Gerade das gemischte Glied 2ab wird beim Auflösen der Klammern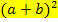 
oder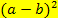 
von vielen Schülern vergessen! Wenn du nicht an die entsprechende Binomische Formel denkst, wirst du genau diesen Fehler begehen!
Herleitung der Binomischen Formeln:
Die Herleitungen der drei Binome sind echt ganz einfach. Man muss eigentlich nur ausmultiplizieren. Bei der Herleitung der ersten beiden Binome muss man allerdings noch daran denken, dass eine Klammer zum Quadrat nichts anderes bedeutet, als die Klammer mit sich selbst multipliziert. (Du weißt sich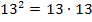er: 
oder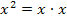 
)
Daher gilt auch: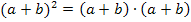 
und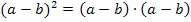 
Den Mal-Punkt darf man bekanntlich auch weglassen. Dann können die Klammern jeweils ausmultipliziert werden:Man muss also jedes Glied der einen Klammer mit Jedem der anderen Klammer multiplizieren. Achte dabei besonders auf die Vorzeichen! (Gleiche Vorzeichen ergeben multipliziert immer Plus;verschiedene Vorzeichen ergeben malgenommen immer Minus!) Durch Zusammenfassen der beiden mittleren Faktoren erhält man dann die jeweilige Binomische Formel.
Herleitung der 1. Binomischen Formel:
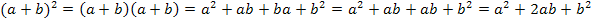
Herleitung der 2. Binomischen Formel:
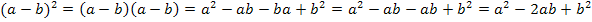
Herleitung der 3. Binomischen Formel:
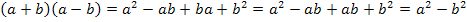
Jetzt bist du vielleicht auf die Idee kommen, dass man doch eigentlich immer so rechnen könnte wie in der gerade gezeigten Herleitung der Formeln. Wozu dann überhaupt die Binome auswendig lernen? Erstens kostet es viel Zeit, wenn man bei jeder Binomischen Formel ausmultipliziert, und zweitens muss man die Umformung auch „rückwärts“ können. Mit „rückwärts“ ist hier gemeint, dass beispielsweise der Ausdruck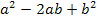 
zu 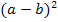umgerechnet werden muss.
Die Binome helfen daher manchmal bei der Umformung einer Summe bzw. Differenz in ein Produkt. Beispielsweise stellt der Ausdruck 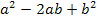die Summe bzw. Differenz dar und der Ausdruck 
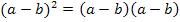das Produkt.
Jede Binomische Formel hat, wie gesagt, eine Summen/Differenzen-Seite und eine Produkt-Seite. Die Umrechnung von der Produkt-Seite in die Summen/Differenzen-Seite kann natürlich auch durch Ausmultiplizieren geschehen;das haben wir ja gerade bei unseren Herleitungen der Binome gemacht. Allerdings dauert das Ausmultiplizieren viel zu lange. Also besser immer die Binomischen Formeln anwenden!
Beispiele:
Produkt 
Summe bzw. Differenz
1. Binomische Formel: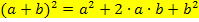 
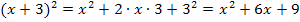
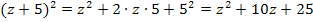
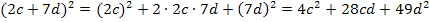
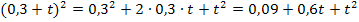
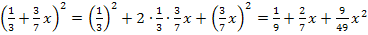
Nur für Schüler, die Wurzeln schon kennen: 
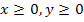
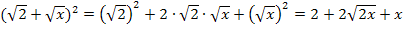
2. Binomische Formel: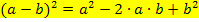 
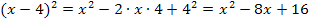
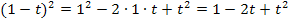
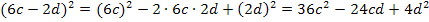
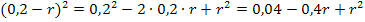
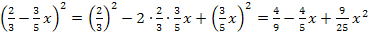
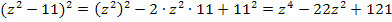
Nur für Schüler, die Wurzeln schon kennen:
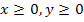
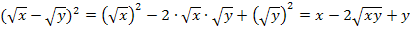
3. Binomische Formel: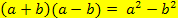 
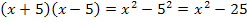
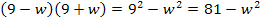
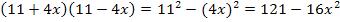
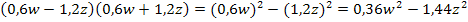
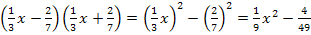
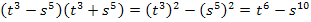
Nur für Schüler, die Wurzeln schon kennen:
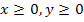
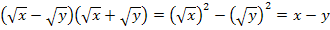
Das Problem bei den Binomen besteht aber besonders darin, auch umgekehrt die Summen/Differenzen-Seite in die Produkt-Seite umwandeln zu können. Genau dafür brauchst du die Binomischen Formeln unbedingt. Das Umwandeln einer Summe bzw. Differenz in ein Produkt nennt man auch Faktorisieren.
