Betrag

Betrag einer Zahl:

Der sogenannte Betrag macht eine Zahl immer positiv. Er wird mit zwei senkrechten Strichen links und rechts neben der Zahl geschrieben:

Bsp.:   

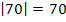
Manchmal ist in mathematischen Texten von Zahlen die Rede, die vom Betrag her großsind. Damit sind Zahlen gemeint, die ohne ihr Vorzeichen große Werte annehmen, die also entweder sehr großoder aber auch sehr klein sind. (Mit „sehr klein“ ist hier gemeint, dass die Zahl sehr weit links auf einem Zahlenstrahl liegt, z.B. -100000.) Sowohl die Zahl  +100000 als auch die Zahl -100000 sind beispielsweise vom Betrag her sehr groß.

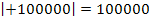
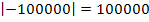
Die beiden Zahlen +100000 und -100000 sind vom Betrag her gleich, d.h. sie unterscheiden sich nur in ihrem Vorzeichen.

Mit der Gleichung 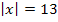ist beispielsweise gemeint, dass x = +13 oder x = -13 sein kann.

Die Ungleichung 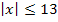beschreibt beispielsweise, dass x zwischen -13 und + 13 liegt, genauer gesagt .

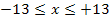Die Ungleichung 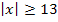beschreibt beispielsweise, dass x höchstens -13 oder mindestens +13 sein soll, also .

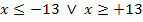Auch in Termen oder Gleichungen können ein oder mehrere Beträge vorkommen.

Beispiel für einen Term mit Betrag: T(x) =

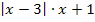
Beispiel für eine Gleichung mit Betrag: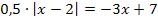       

Um solche Terme zu vereinfachen oder derartige Gleichungen zu lösen, ist eine sogenannte Fallunterscheidung nötig. Je nachdem, ob das Argument des Betrages (das, was innerhalb der Betragsstriche steht) positiv oder negativ ist, muss unterschiedlich vorgegangen werden.

Ist das Argument positiv oder gleich Null, kann der Betrag durch eine Klammer ersetzt werden oder manchmal einfach weggelassen werden. Ist das Argument negativ, dreht man entweder alle Vorzeichen des Arguments um und setzt dann statt dem Betrag wieder eine Klammer oder man ersetzt den Betrag durch eine Klammer mit einem Minuszeichen davor.

Ob das Argument (das, was innerhalb der Betragsstriche steht) positiv oder negativ ist, hängt aber oft von x ab.  Betrachten wir beispielsweise 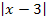. Das Argument x – 3 ist positiv oder gleich Null, wenn für x eine Zahl eingesetzt wird, die größer oder gleich 3 ist. Setzt man dagegen für x Zahlen ein, die kleiner sind als 3, wird der Ausdruck x – 3  negativ. Soll der Betrag 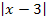aufgelöst werden, müssen daher die beiden Fälle 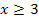und 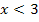unterschieden werden. Um z.B. den Term T(x) = 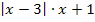zu vereinfachen, müssen wir ihn betragsfrei schreiben und dazu brauchen wir die Fallunterscheidung.

Für 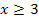ist das Argumen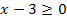t Die Betragsstriche werden durch eine Klammer ersetzt.

Für 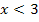ist das Argumen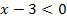t Die Betragsstriche werden durch eine Klammer mit Minuszeichen davor ersetzt oder es werden alle Vorzeichen des Arguments umgedreht und dann eine Klammer herum gesetzt.

Oft wird die im Folgenden gezeigte Schreibweise mit geschweifter Klammer gewählt.

T(x) =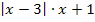

T(x) =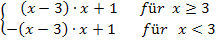

T(x) =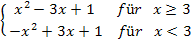

Fallunterscheidungen bei Betragsgleichungen findest du im Bereich Algebra im Kapitel Betragsgleichungen.

Betragsfunktion:

Der Betrag kann auch in Funktionsgleichungen auftauchen. Unter der Betragsfunktion versteht man die folgende Funktion:

f(x) = 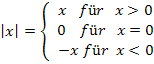oder kürzer geschrieben:  f(x) =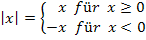

Der Graph der Betragsfunktion entsteht durch Kombination der Funktionen y = x (steigende Winkelhalbierende) für 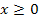und y = – x (fallende Winkelhalbierende) für .

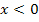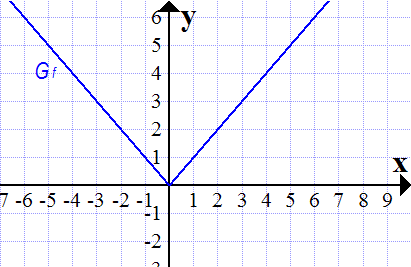
Graph der Funktion f(x) =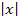

Wichtig für Schüler der Oberstufe eines Gymnasiums oder der FOS bzw. BOS:

An der Stelle x = 0 hat der Graph der Betragsfunktion einen Knick bzw. eine Spitze. Die Steigung kann daher an der Stelle x = 0 nicht angegeben werden.

Man sagt:An der Stelle x = 0 ist die Funktion f nicht differenzierbar. Genaueres dazu im Bereich Analysis im Kapitel Stetigkeit und Differenzierbarkeit.

Mehr zur Betragsfunktion oder zu Funktionen, deren Gleichung einen oder mehrere Beträge enthalten, findest du im Bereich Analysis im Kapitel Betragsfunktion, Signumfunktion und Gaußsche Treppenfunktion. Dort wird auch auf die notwendigen Fallunterscheidungen beim Rechnen mit Betragsfunktionen ausführlich eingegangen.

Betrag eines Vektors:

Vom Betrag einer Zahl, z.B. 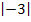, ist der Betrag eines Vektors, z.B. 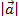mit 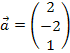,  zu unterscheiden. Ein Vektor beschreibt die Menge aller parallelgleicher Pfeile, also einen Pfeil, den man verschieben darf. Unter dem Betrag eines Vektors versteht man seine Länge, d.h. die Länge des Pfeiles.

Wie der Betrag 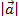eines Vektors 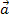berechnet wird, hängt davon ab, ob man in einem zwei- oder dreidimensionalen Koordinatensystem arbeitet. (Realschüler müssen nur im zweidimensionalen x,y-Koordinatensystem rechnen können;alle Schüler eines Gymnasiums, der FOS oder BOS (jeweils technischer Zweig) müssen ab der Oberstufe auch im dreidimensionalen Koordinatensystem rechnen können.)

Zweidimendionales x,y-Koordinatensystem:

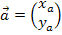
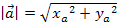
Bsp.:

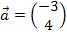
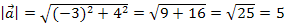
Der Vektor 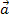hat also eine Länge von 5 LE (Längeneinheiten).

Dreidimensionales 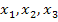-Koordinatensystem:

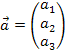
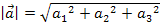
Bsp.:

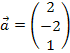
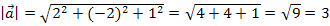
Der Vektor 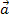hat also eine Länge von 3 LE (Längeneinheiten).

---