Bestimmtes Integral
Das bestimmtes Integral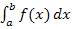 
entspricht der Fläche zwischen dem Graph 
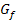der Funktion 
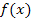, den senkrechten Geraden x = a und x = b sowie der x-Achse, wenn die Fläche vollständig oberhalb der x-Achse liegt. Die Funktion 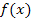, die integriert werden soll, heißt Integrand oder Integrandenfunktion.
Der Ausdruck „dx“, der beim Integral immer hinter die Integrandenfunktion geschrieben wird, gibt an, dass nach x integriert werden muss;d.h. dass x die Variable ist.
Die Zahl a stellt die untere Grenze des Integrals 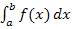und b die obere Grenze dar. Das bedeutet anschaulich, dass die senkrechte Gerade 
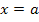die Fläche auf der linken Seite begrenzt und die zweite senkrechte Gerade 
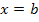die Fläche auf der rechten Seite begrenzt. Vergleiche Skizze!
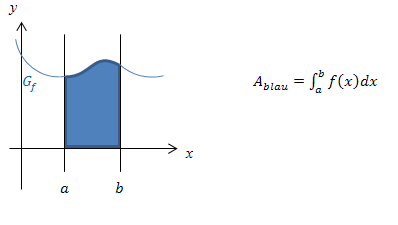
Liegt die Fläche komplett oberhalb der x-Achse, ist das Integral positiv und sein Wert entspricht dem Flächeninhalt zwischen 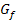und der x-Achse von x = a bis x = b.
Liegt die Fläche dagegen komplett unterhalb der x-Achse, ist das Integral negativ. Ein Flächeninhalt kann natürlich nicht negativ sein. Erst der Betrag des Integrals entspricht dann dem Flächeninhalt zwischen 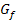und der x-Achse von x = a bis x = b.
Das bestimmte Integral ist also nicht immer das gleiche wie der Flächeninhalt derjenigen Fläche, die durch den Graphen 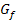, die senkrechten Geraden x = a und x = b sowie der x-Achse begrenzt ist. Das bestimmte Integral entspricht streng genommen der sogenannten Flächenbilanz. Dabei werden die unterhalb der x-Achse liegenden Flächenanteile negativ gezählt, die oberhalb der x-Achse liegenden Flächenanteile aber positiv. Die Flächenbilanz ist gleich Null und somit auch das bestimmte Integral, wenn die Flächenanteile oberhalb und unterhalb der x-Achse gleich großsind.
Berechnung eines bestimmten Integrals:
· Stammfunktion bilden
· Grenzen einsetzen (Obere minus untere)
Berechnet wird ein bestimmtes Integral, indem man in einem ersten Schritt eine Stammfunktion F(x) bildet und diese in eckige Klammern schreibt (die Grenzen werden dabei oben und unten an die rechte Klammer geschrieben).
