Bedingte Wahrscheinlichkeit

Unter einer bedingten Wahrscheinlichkeit versteht man eine Wahrscheinlichkeit, die nur gilt, wenn eine bestimmte Voraussetzung (Bedingung) erfüllt ist. Für die Wahrscheinlichkeit, dass das Ereignis B eintritt, wenn das Ereignis A eingetreten ist, schreibt man: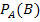

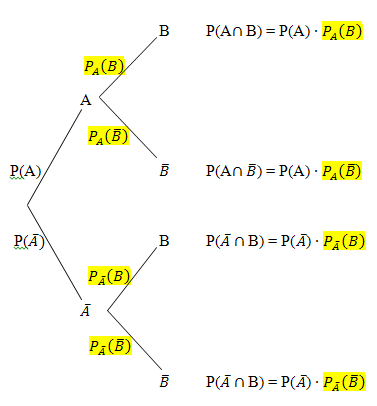
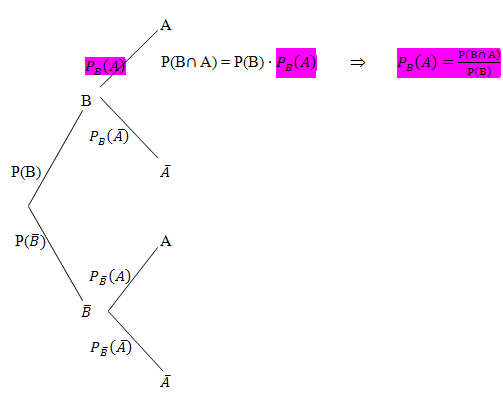
Im Baumdiagramm stehen die bedingten Wahrscheinlichkeiten immer an den hinteren Verzweigungen. Alle bedingten Wahrscheinlichkeiten sind im nachfolgenden Baumdiagramm gelb markiert.

Berechnet wird die bedingte Wahrscheinlichkeit 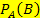nach der Formel: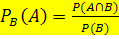

Woher diese Formel kommt, lässt sich leicht mit dem Baumdiagramm nachvollziehen. Nach der 1. Pfadregel gilt, dass die Wahrscheinlichkeiten entlang eines Pfades an Baumdiagram-men multipliziert werden müssen, um die Wahrscheinlichkeit P(A 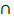B) des Ereignisses A und zugleich B zu erhalten. Die UND-Wahrscheinlichkeit P(A 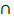B) steht im oben dargestellten Baumdiagramm am Ende des obersten Pfades. Nach der 1. Pfadregel berechnet sie sich folgendermaßen:

P(A 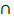B) = P(A)

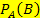
Durch Umstellen nach 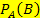erhält man die oben gezeigte Formel für die bedingte Wahrscheinlichkeit.

P(A 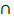B) = P(A) |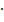

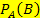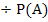
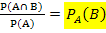
Alle anderen bedingten Wahrscheinlichkeiten können entsprechend an den anderen Pfaden berechnet werden.

In vielen Aufgaben sind die Wahrscheinlichkeiten P(A), 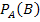und 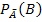gegeben und die umgekehrte bedingte Wahrscheinlichkeit 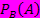ist gesucht.

Um diese Art von Aufgaben lösen zu können, verwendet man zusätzlich ein zweites Baumdiagramm, bei dem nun B bzw. 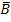vorne und A bzw. 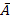hinten steht. Nur in diesem Baumdiagramm lässt sich die gesuchte bedingte Wahrscheinlichkeit 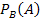eintragen. Siehe Baumdiagramm unten!

Um mit der Formel 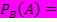 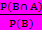    , die sich am obersten Pfad dieses Baumdiagramms herleiten lässt, die gesuchte bedingte Wahrscheinlichkeit 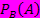berechnen zu können, braucht man die Wahrscheinlichkeiten P(B 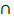A) und P(B). Die Wahrscheinlichkeit P(B 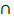A) ist gleich der Wahrscheinlichkeit P(A 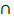B), die man aus dem ursprünglichen Baumdiagramm mit der 1. Pfadregel ermitteln kann. Die Totale Wahrscheinlichkeit P(B) berechnet man entweder mit einer Vierfeldertafel oder einfach mit P(B) = P(A 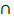B) + P( 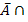B), wobei sich P( 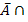B) aus dem ursprünglichen Baumdiagramm wieder nach der 1. Pfadregel ergibt.

Mehr zu diesem Thema und konkrete Aufgabenbeispiele findest du im Bereich Stochastik im Kapitel Bedingte Wahrscheinlichkeit.