Baumdiagramm

Ein Baumdiagramm ist eine übersichtliche, graphische Darstellung, die in der Stochastik, d.h. in der Wahrscheinlichkeitsrechnung, oft verwendet wird. Vor allem bei zusammengesetzten Zufallsexperimenten bietet es sich an ein Baumdiagramm zu zeichnen.

Beispiel:

Gegeben ist eine Urne mit 3 blauen, 1 gelben und 5 roten Kugeln. Alle Kugeln sind gleich großund unterscheiden sich nur in ihrer Farbe. Es wird zweimal ohne Zurücklegen gezogen. Es soll für dieses Zufallsexperiment ein Baumdiagramm gezeichnet und der Ergebnisraum 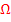angegeben werden.

Wir verwenden die Abkürzungen b für blaue Kugel, g für gelbe Kugel und r für rote Kugel.

Baumdiagramme können auf zwei verschiedene Art und Weisen gezeichnet werden, entweder werden die einzelnen Pfade übereinander oder nebeneinander gezeichnet. Du machst es einfach, wie dein Lehrer in der Schule!

Hier siehst du das Baumdiagramm mit den Ereignissen nebeneinander:

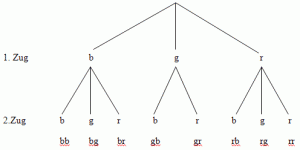
Nun siehst du das verlangte Baumdiagramm in der anderen Form:

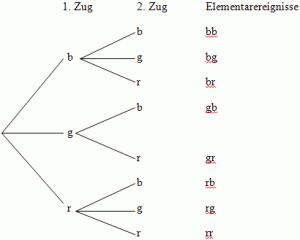
Ergebnisraum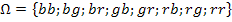

Beachte, dass ohne Zurücklegen gezogen wird! Das hat zur Folge, dass jede Kugel nur einmal gezogen werden kann. Hat man beispielsweise die einzige gelbe Kugel beim ersten Zug schon gezogen, kann sie beim zweiten Zug nicht mehr gezogen werden. Deshalb dürfen im Baumdiagramm von g ausgehend nur zwei Pfade gezeichnet werden, nämlich der zu b und zu r. (Vergleiche erstes Baumdiagramm Bereich unten Mitte bzw. im zweiten Baumdiagramm Mitte hinten!) Dagegen gehen von b und von r jeweils drei Äste weg. Da sowohl von den blauen Kugeln als auch von den roten Kugeln ursprünglich mehr als eine in der Urne waren, kann beim zweiten Zug noch einmal eine blaue bzw. eine rote Kugel kommen. In anderen Worten:Es gibt zwar die beiden Fälle bb und rr, aber nicht gg. (Hätte man mit Zurücklegen gezogen, hätte auch der Fall gg existiert. Dann wären auch von g drei Äste weggegangen.)

Mehr zu diesem Thema im Bereich Stochastik im Kapitel Baumdiagramm.

Wenn du dich auch dafür interessierst, wie man mit Hilfe von Baumdiagrammen die Wahrscheinlichkeiten der Elementarereignisse berechnet, gehe in den Bereich Stochastik in das Kapitel Laplace-Wahrscheinlichkeit.