Asymptote
Unter einer Asymptote versteht man eine Gerade, an die sich der Graph einer Funktion anschmiegt, die er aber (zumindest in diesem Bereich, wo sie gilt) nicht schneidet oder berührt. Der Graph nähert sich also beliebig nah an die Asymptote an, erreicht sie jedoch nicht. Asymptoten können waagrecht, senkrecht oder sogar schräg verlaufen.
Beispiel: f(x) = 
Der Graph der Funktion f(x) =  ist eine sogenannte Hyperbel. Siehe Abbildung! Er schmiegt sich einerseits für vom Betrag her sehr große x-Werte an die x-Achse an und andererseits für betragsmäßig sehr kleine x-Werte an die y-Achse an. Die Funktion hat also sowohl eine senkrechte als auch eine waagrechte Asymptote.
ist eine sogenannte Hyperbel. Siehe Abbildung! Er schmiegt sich einerseits für vom Betrag her sehr große x-Werte an die x-Achse an und andererseits für betragsmäßig sehr kleine x-Werte an die y-Achse an. Die Funktion hat also sowohl eine senkrechte als auch eine waagrechte Asymptote.
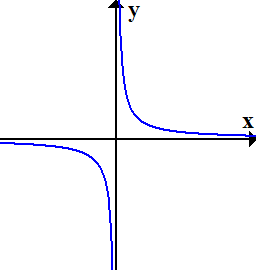
Der Graph der Funktion f(x) =  , eine sogenannte Hyperbel.
, eine sogenannte Hyperbel.
Wie die Gleichungen von Asymptoten ermittelt werden, wird im Bereich Analysis in den Kapiteln Gebrochenrationale Funktionen, Exponential- und Logarithmusfunktionenund Grenzwerte:Verhalten im Unendlichen und an den Definitionslücken ausführlich erklärt.

