Äquivalenzumformung
Eine Äquivalenzumformung ist eine Umformung einer Gleichung, welche die Lösungsmenge der Gleichung nicht verändert. Man verwendet Äquivalenzumformungen, wenn man eine Gleichung nach x auflösen will. Du kennst das ganz bestimmt. Meist macht man rechts hinter der Gleichung in einem gewissen Abstand einen senkrechten Strich und schreibt dahinter, welche Umformung vorgenommen wird. Im Prinzip wird die Rechenoperation auf beiden Seiten der Gleichung vorgenommen;daher ändert sich nichts an der Lösungsmenge der Gleichung. (Man kann sich die Gleichung dabei als Balkenwaage vorstellen:Fügt man beispielsweise auf beiden Seiten gleich viel hinzu, kippt die Waage nicht. Das gleiche gilt, wenn man auf beiden Seiten gleich viel wegnimmt.) Nur am Anfang, wenn man gerade erst lernt, Gleichungen mittels Äquivalenzumformungen nach x aufzulösen, schreibt man die Rechenoperation wirklich auf beiden Seiten der Gleichung hin. Später lässt man diesen Zwischenschritt einfach weg. Man hat ja gelernt, dass ein Plus-Ausdruck mit Minus auf die andere Seite der Gleichung kommt, und dass ein Minus-Ausdruck mit Plus auf die andere Seite gebracht wird. Entsprechend wird ein Mal-Ausdruck mit geteilt auf die andere Seite gebracht und umgekehrt ein Geteilt-Ausdruck mit mal. Diese Erklärung ist zwar absolut „unmathematisch“, doch hast du bestimmt verstanden, was damit gemeint ist, denn so wirst du das sicher schon längere Zeit machen, genauer gesagt seit der 7. Klasse.
Hier ein einfaches Beispiel einer Gleichung, die mit Äquivalenzumformungen nach x aufgelöst wird:
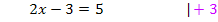
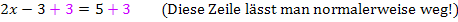
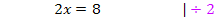


Viele Schüler haben anfangs Probleme, Gleichungen nach x aufzulösen, wenn x im Nenner steht. Gleichungen mit x im Nenner nennt man Bruchgleichungen. Sie werden im G8 Ende der 8. Klasse im Unterricht genauer behandelt.
Merke:Steht x im Nenner, musst du immer mit dem Nenner multiplizieren, um die Gleichung nach x aufzulösen.
Beispiel einer einfachen Gleichung mit x im Nenner:
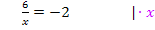
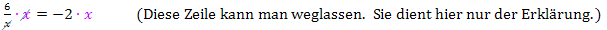

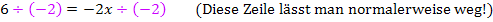
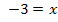
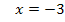
Ausführlichere Erklärungen zu Gleichungen, die x im Nenner enthalten, findest du im Kapitel Bruchgleichungen.

