Äquivalente Gleichungen
Zwei Gleichungen heißen äquivalent, wenn sie die gleiche Lösungsmenge besitzen. (Die Lösungsmenge enthält alle Zahlen der Grundmenge, die für x in die Gleichung eingesetzt eine wahre Aussage ergeben.)
Z.B. sind die beiden Gleichungen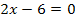 
und 
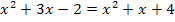äquivalent. Man erkennt dies, wenn man die beiden Gleichungen mittels Äquivalenzumformungen nach x auflöst.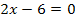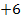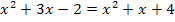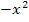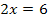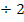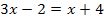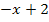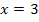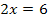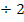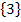
| 
| 
| 
| 
|
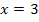
L = 
L =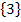
Die beiden Gleichungen haben beide die gleiche Lösungsmenge. Deshalb sind sie äquivalent.
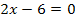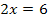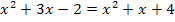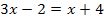Auch die Gleichungen und sind äquivalent zueinander, da sie durch eine Äquivalenzumformung ineinander umgewandelt werden können. Das gleiche gilt auch für die Gleichungen und sowie 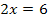. Durch Äquivalenzumformungen entstehen immer äquivalente Gleichungen.
