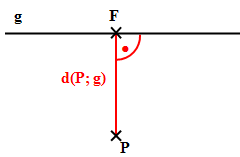
Abstand: Punkt – Gerade

Unter dem Abstand eines Punktes von einer Geraden versteht man die kürzeste Entfernung eines Punktes von einer Geraden. Die mathematische Schreibweise für den Abstand eines Punktes P von einer Geraden g ist d(P; g), wobei das d von Distanz bzw. distance (engl.) kommt. Um den Abstand d(P; g) einzuzeichnen, fällt man vom Punkt P aus dasLot auf die Gerade g. (Das Lot ist eine zur Gerade g senkrechte Gerade.) Der Abstand wird also immer senkrecht zur Gerade eingezeichnet.

Der Punkt, wo das Lot die Gerade g schneidet, wird als Lotfußpunkt bezeichnet. Auf dieser website wird der Lotfußpunkt immer mit F, wie Fußpunkt, bezeichnet; das ist auch allgemein üblich. (In manchen Lehrbüchern findet sich statt F aber auch die Bezeichnung L.) Der Abstand des Punktes P von der Gerade g entspricht dann der Länge der Strecke [PF].

Wie sich der Abstand d(P; g) eines Punktes P von einer Geraden g berechnen lässt, hängt davon ab, ob man in einem zwei- oder dreidimensionalen Koordinatensystem rechnet. Näheres zur Berechnung von d(P; g) mit Hilfe der analytischen Geometrie findest du in den Kapiteln Abstand: Punkt – Gerade (im  ) und Abstand: Punkt – Gerade (im  ).

---