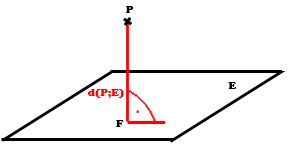
Abstand: Punkt – Ebene
Unter dem Abstand eines Punktes von einer Ebene versteht man die kürzeste Entfernung eines Punktes von einer Ebene. Die mathematische Schreibweise für den Abstand eines Punktes P von einer Ebene E ist d(P; E), wobei das d von Distanz bzw. distance (engl.) kommt. Um den Abstand d(P; E) in einer Skizze einzuzeichnen, fällt man vom Punkt P aus das Lot auf die Ebene E. (Das Lot ist eine zur Ebene E senkrechte Gerade.) Der Abstand wird also immer senkrecht zur Ebene eingezeichnet.
Der Punkt, in dem das Lot die Ebene E schneidet, wird als Lotfußpunkt bezeichnet. Auf dieser website wird der Lotfußpunkt immer mit F, wie Fußpunkt, bezeichnet; das ist auch allgemein üblich. (In manchen Lehrbüchern findet sich statt F aber auch die Bezeichnung L.) Der Abstand des Punktes P von der Ebene E entspricht dann der Länge der Strecke [PF].
Wie sich der Abstand d(P; E) eines Punktes P von einer Ebene E berechnen lässt, hängt davon ab, ob man nur den Abstand oder zusätzlich auch den Lotfußpunkt berechnen soll. Besonders hilfreich bei der Berechnung des Abstands eines Punktes von einer Ebene ist die sogenannte Hesse-Normalenform einer Ebene. Sie liefert jedoch nur den Abstand d(P; E), nicht aber den Lotfußpunkt F. Näheres zur Berechnung von d(P; E) mit Hilfe der analytischen Geometrie findest du im Kapitel Abstand: Punkt – Ebene.