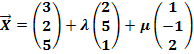Zwei sich schneidende Geraden
3. Zwei sich schneidende Geraden g und h, die in der Ebene liegen sollen
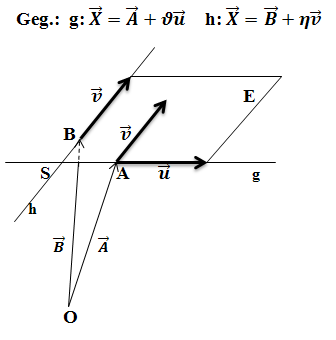
Anmerkung zur Skizze:Die Geraden g und h liegen eigentlich nicht am Rand der Ebene, auch wenn das in der Skizze so aussieht. Sie liegen eigentlich irgendwo innerhalb der Ebene. Eine Ebene hat bekanntlich gar keinen Rand, sie geht unendlich weiter! Diese Art der Darstellung wurde nur ihrer Einfachheit wegen gewählt. Diese Skizze soll nur veranschaulichen, wie man eine Ebenengleichung aufstellen kann, wenn zwei sich schneidende Geraden gegeben sind, die in der Ebene liegen sollen.
Als Aufpunkt der Ebene kann bekanntlich jeder beliebige Ebenenpunkt verwendet werden. Da die beiden Geraden g und h in der Ebene E liegen, liegen auch die Aufpunkte der beiden Geraden in der Ebene. Daher kann entweder der Aufpunkt der Gerade g, hier mit A bezeichnet, oder der Aufpunkt der Gerade h, hier B genannt, als Aufpunkt der Ebene E verwendet werden. Man könnte natürlich auch den Schnittpunkt S der beiden Geraden als Aufpunkt der Ebene verwenden, doch wäre das sehr umständlich, wenn man den Schnittpunkt S erst noch berechnen muss. Wir nehmen nun den Punkt A als Aufpunkt der Ebene.
Zusätzlich benötigen wir noch zwei Richtungsvektoren, um die Ebene E in Parameterform aufstellen zu können. Wir verwenden einfach die beiden Richtungsvektoren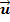 
und 
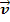der beiden Geraden. Da sich die beiden Geraden schneiden, sind die Richtungsvektoren der beiden Geraden sicherlich keine Vielfachen voneinander. Da beide Geraden in der Ebene E liegen, spannen 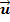und 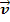die gesuchte Ebene auf.
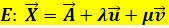
Man hätte natürlich auch B oder den Schnittpunkt S der beiden Geraden als Aufpunkt der Ebene E verwenden können:
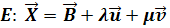
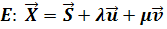
Merke:Um mit zwei sich schneidenden Geraden eine Ebenengleichung in Parameterform aufzustellen, nimmt man einfach einen der beiden Aufpunkte und die beiden Richtungsvektoren der Geraden. Den zweiten Aufpunkt braucht man gar nicht;er wird einfach weggelassen.
Vorsicht:Bei parallelen Geraden funktioniert das nicht! Sind die beiden gegebenen Geraden echt parallel, legen sie zwar auch eine Ebene E eindeutig fest, jedoch dürfen dann die Richtungsvektoren der Geraden nicht beide als Richtungsvektoren der Ebene verwendet werden, da sie Vielfache voneinander sind. Die Richtungsvektoren einer Ebene dürfen aber keinesfalls Vielfache voneinander sein. Zwei Vektoren, die Vielfache voneinander sind, spannen schließlich keine Ebene auf! Wie man mit parallelen Geraden eine Ebenengleichung aufstellt, wird weiter unten noch ausführlich erklärt. Sollst du mit zwei gegebenen Geraden eine Ebenengleichung aufstellen, musst du also unbedingt vorher die Lagebeziehung zwischen den beiden Geraden überprüfen. Schneiden sich die beiden Geraden, geht man wie oben beschrieben vor, d.h. man wählt einen Aufpunkt der Geraden aus, macht ihn zum Aufpunkt der Ebene und verwendet die beiden Richtungsvektoren der Geraden als Richtungsvektoren der Ebene. Bei parallelen Geraden muss man jedoch anders vorgehen. Siehe unten!
Bsp.:Ermittle eine Gleichung der Ebene E in Parameterform, welche
die Geraden g und h enthält!
g: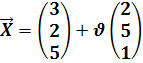 
h: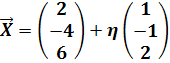 
Lösung:
Wir bezeichnen wie bisher den Aufpunkt der Gerade g mit A und den Richtungsvektor von g mit 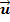. Den Aufpunkt der Gerade h nennen wir wieder B und den Richtungsvektor .
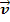Geg.: g: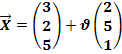 
h: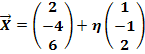 
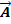
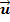
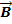
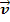
Zuerst muss die Lagebeziehung der beiden Geraden g und h untersucht werden. Die Richtungsvektoren 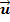und 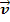sind offensichtlich keine Vielfachen voneinander. Daher können die Geraden nicht parallel oder identisch sein. Sie können sich also nur noch schneiden oder windschief sein. In der Aufgabe ist nach einer Ebene gefragt, die beide Geraden enthalten soll;das ist nur mit zwei sich schneidenden Geraden möglich, nicht aber mit zwei windschiefen Geraden. Daher sparen wir uns den rechnerischen Nachweis, dass sich die Geraden schneiden. (Streng genommen müsste man das noch beweisen, bevor die Ebenengleichung aufgestellt wird. Den rechnerischen Nachweis, dass sich zwei Geraden schneiden, findest du im Kapitel Lagebeziehungen zweier Geraden im 
)
Da man nun weiß, dass sich die Geraden g und h schneiden, lässt sich die Parameterform der Ebene, die die beiden Geraden enthält, leicht aufstellen. Man nimmt einen der beiden Aufpunkte, beispielsweise A, und die beiden Richtungs-vektoren 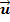und 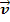. Den zweiten Aufpunkt B braucht man nicht, um die Ebenengleichung aufzustellen. Im Prinzip kann die Gleichung der einen Gerade abgeschrieben und der Richtungsvektor der zweiten Gerade einfach dahinter gesetzt werden. Nur die Parameter sollten durch andere Buchstaben ersetzt werden, um eventuelle Verwechslungen der Parameter der Geraden mit denen der Ebene in folgenden Rechnungen zu vermeiden.
Noch einmal die Angabe: g: 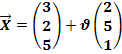h: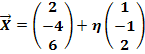
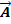
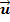
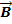
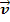
E: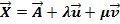 
E: 
